HY03

HY03

저는 전문가가 아니고 이것 저것 알아보는 비전문가 입니다.
틀린 내용이 기술되어도 너그러이 봐주시고 댓글을 남겨주셨으면 좋겠습니다.

Prediction and Control with Function Approximation - 01. Week 1. On-policy Prediction with Approximation

강의 개요 (과정 로드맵)

  • 가치함수를 테이블로 표현할 수 있는 경우

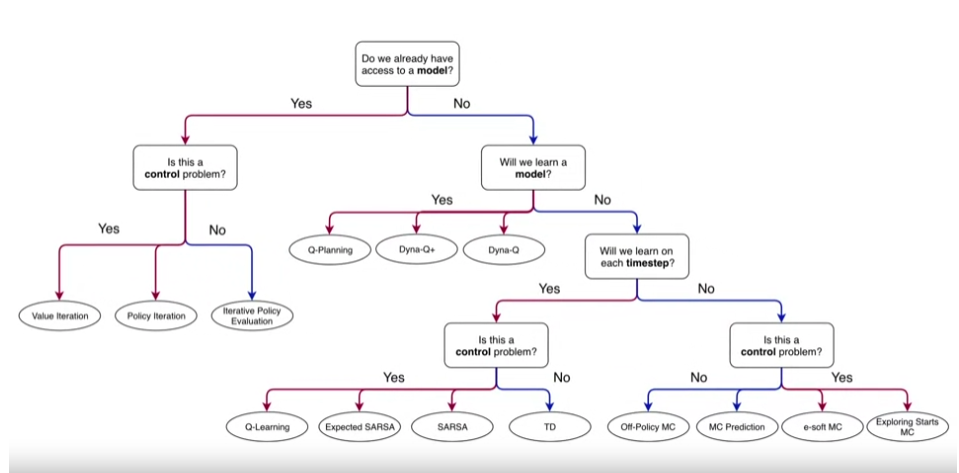
categorize_reinforcement_learning_1

  • 가치함수를 테이블로 표현할 수 없는 경우

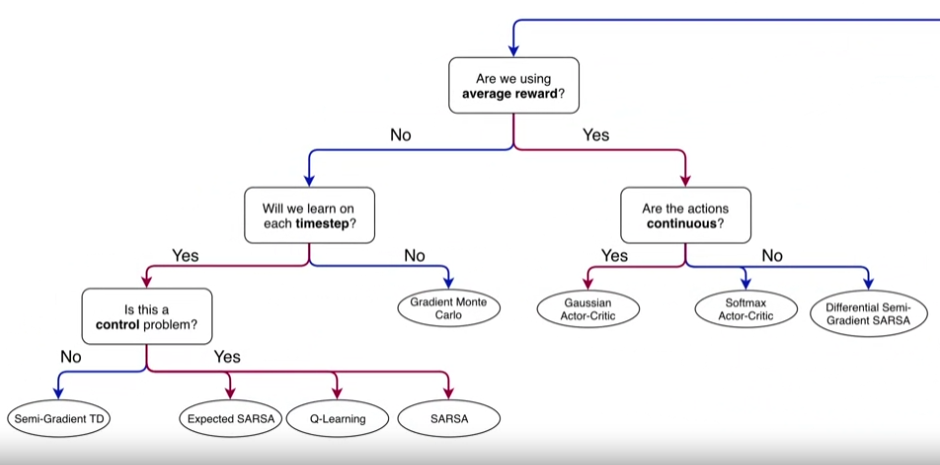
categorize_reinforcement_learning_2

관련 자료 (RLbook Pages 197-209)

  • On-policy Prediction with Approximation (개요)
    • 이 장에서는 강화학습의 함수 근사의 학습을 다룬다.
      • 함수 근사는 On-policy 데이터의 상태가치함수를 추정하기 위해 사용
      • 즉, 알고있는 정책 $\pi$ 로 생성한 경험으로 $v_\pi$ 를 근사하고자 한다.
    • 여기에서 눈여겨볼 점은 가치 함수 근사는 테이블로 나타내지 않고, 파라미터화된 함수의 형태 (벡터 $\textbf{w}$ $\in \mathbb{R}^d$) 를 사용한다는 점이다.
    • $\hat{v}(s,$ $\textbf{w}) \approx v_\pi(s)$
      • 상태 $s$ 와 주어진 가중치 벡터 $\textbf{w}$ 의 근사된 값을 나타냄
      • $\hat{v}$ 는 상태의 요소에 대한 선형함수일 수 있고, $\textbf{w}$ 는 요소에 대한 가중치 벡터일 수 있음.
      • 더 일반적으로 $\hat{v}$ 는 다중 인공 신경망 (multi-layer artificial neural network) 에 의해 계산되는 함수일 수 있고, $\textbf{w}$ 는 모든 층에 연결된 가중치일 수 있음.
      • 혹은 $\hat{v}$ 는 의사결정나무 (decision tree) 에 의해 계산되는 함수일수 있고, $\textbf{w}$ 는 모든 분기점과 트리의 리프 값을 정의하는 모든 숫자일 수 있음.
    • 일반적으로 가중치의 수 ($\textbf{w}$ 의 차원 수) 는 상태의 수보다 훨씬 작고 ($d \ll | \mathcal{S} |$), 하나의 가중치의 변화는 다수의 상태의 예측값을 바꾸게 된다.
      • 따라서 하나의 상태가 업데이트되면 일반화되어, 다른 다수의 상태의 값에 영향을 주게 된다.
      • 이러한 일반화 (generalization) 는 학습을 더욱 강력하게 하는 동시에 이해와 관리를 어렵게 한다.
    • 놀랍게도 강화학습을 함수 근사로 확장하면 전체 상태를 사용할 수 없는 부분적으로 관찰이 가능한 문제에도 적용할 수 있다.
      • $\hat{v}$ 에 대한 파라미터화된 함수 형식이 추정값이 상태의 특정 요소에 의존하는 것을 허용하지 않으면, 이는 해당 측면을 관찰할 수 없는 것과 같다.
      • 실제로 이 책의 이 부분에 제시된 함수 근사를 사용하는 이론적 결과물은 부분적 관찰의 케이스에도 잘 적용된다.
    • 그러나 함수 근사가 할 수 없는 것은 과거 관찰에 대한 기억으로 상태의 표현을 강화하는 것이다.
      • 이러한 부분의 일부는 섹션 17.3 에서 간략하게 논의하기로 한다.
  • Value-function Approximation
    • 이 책의 모든 예측 방법 (prediction methods) 은 특정 상태의 값을 backed-up value 혹은 update target 으로 이동시키는, 추정 가치 함수 (estimated value function) 의 업데이트이다.
    • 개개의 업데이트를 표기법 $s \mapsto u$ 로 나타내도록 한다.
      • $s$ 는 상태 업데이트를 뜻하고, $u$ 는 $s$ 의 추정값이 향하는 update target 을 뜻한다.
      • Monte Carlo update : $S_t \mapsto G_t$
      • TD update : $S_t \mapsto R_{t+1} + \gamma \hat{v} (S_{t+1},$ ${\textbf{w}}_t)$
      • n-step TD update : $S_t \mapsto G_{t:t+n}$
      • DP policy-evaluation update : $s \mapsto$ $E_{\pi}$ $[ R_{t+1} + \gamma \hat{v} (S_{t+1},$ ${\textbf{w}}_t)$ $| S_t = s ]$
        • $s$ 는 임의의 상태를 뜻하며, $S_t$ 는 실제 경험에서 마주하게 된 상태를 의미한다.
    • 지금까지의 실제 업데이트는 $s$ 의 추정 값에 대한 테이블 항목이 $u$ 방향으로 약간 이동되며, 다른 모든 상태의 추정값은 변경되지 않은 채로 남아 있었음.
    • 이제는 업데이트를 구현하기 위해 임의로 복잡하고 정교한 방법을 허용, $s$ 에서의 업데이트는 다른 많은 상태의 추정 값도 변경되도록 일반화한다.
      • 이러한 방식으로 입력-출력 예제를 모방하는 방법을 학습하는 기계 학습 방법을 지도 학습 방법 (Supervised learning) 이라고 한다.
      • 출력이 $u$ 와 같은 숫자인 경우 이 프로세스를 종종 함수 근사라고 한다.
      • 우리는 각 업데이트의 $s \mapsto g$ 를 훈련 예제로 전달하여 값의 예측을 위해 이러한 방법을 사용한다.
      • 그런 다음 그들이 생성하는 근사 함수를 가치 추정 함수로 본다.
    • 이러한 방식으로 각 업데이트를 전통적인 학습 예제로 보면, 가치 예측을 위한 광범위한 함수 근사 방법을 사용할 수 있다.
      • 원칙적으로, 인공신경망, 의사결정트리, 다양한 종류의 다변량 회귀 등 다양한 지도학습의 학습 방법을 모두 사용 가능
      • 그러나 모든 함수 근사 방법이 강화 학습에 사용하기 적합한 것은 아님.
        • 정교한 인공신경망과 통계 방법은 다중 패스가 이루어지는 정적 훈련 세트를 가정한다.
        • 그러나 강화학습에서는 에이전트가 환경 혹은 환경 모델과 상호작용하는 동안 학습이 온라인으로 이루어질수 있다는 것이 중요
        • 이를 위해 점진적으로 획득된 데이터로부터 효율적으로 학습할 수 있는 방법이 필요함.
      • 또한 강화학습에서는 일반적으로 비정상성 (nonstationary target) (시간에 따라 변하는 목표) 를 처리할 수 있는 함수 근사 방법이 필요함.
        • 예를 들어 GPI (generalized policy iteration) 기반 방법에서는 $\pi$ 가 변경되는 동안 $q_\pi$ 를 학습하려고 하는 경우가 많음.
        • 정책이 동일하게 유지되더라도 훈련 예제의 목표 값이 부트스트래핑 방법 (DP, TD 등) 으로 생성된 경우 비정상성임.
        • 이러한 비정상성을 쉽게 처리할 수 없는 방법은 강화학습에 적합하지 않다.
  • The Prediction Objective ($\overline{VE}$)
    • 예측을 위한 명시적인 목표
      • Tabular case 의 경우
        • 예측을 위한 명시적인 목표를 지정하지 않았음.
        • 학습된 가치함수가 실 가치함수와 정확하게 동일해질 수 있기 때문에 예측 품질에 대한 지속적인 측정이 필요하지 않음.
        • 각 상태에서 학습된 값들은 서로 분리되어있었음 (한 상태의 업데이트가 다른 상태에 영향을 주지 않음)
      • Function Approximation 의 경우
        • 근사를 사용하면 한 상태의 업데이트가 다른 많은 상태에 영향을 미치므로 모든 상태의 값을 정확하게 얻는 것은 불가능
        • 가중치보다 훨씬 더 많은 상태가 있으므로, 한 상태의 추정치를 정확하게 만드는 것은 다른 상태의 추정치를 덜 정확하게 만드는 것을 의미
        • 이는 어떤 상태에 집중할 지를 정해야 함을 의미
    • Mean Squared Value Error, $\overline{VE}$
      • 즉, $\mu (s)$ 를 정의해야 함.
        • 상태의 분포 $\mu (s) \geq 0, \sum_s \mu(s) = 1$
        • 각 상태 $s$ 의 오차에 대해 얼마나 신경 써야할지를 의미
      • 상태 $s$ 에서의 오차는 근사값 $\hat{v} (s,$ $\textbf{w})$ 와 참 값 $v_\pi(s)$ 의 차의 제곱을 의미한다.
        • 이를 각 상태별 $\mu$ 를 이용해 가중치를 부여하면 아래의 식이 도출됨.

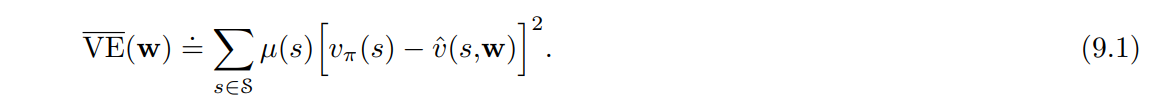
      9_2_1_VE

      • $\overline{VE}($$\textbf{w}) \doteq \sum_{s \in S} \mu(s)$ $[ v_\pi(s) - \hat{v} (s,$ $\textbf{w}) ]^2$
        • 이 측정값의 제곱근, root $\overline{VE}$ 는 근사값과 실제 값이 얼마나 다른지에 대한 대략적 측정값을 제공하며 도표에서 자주 사용됨.
        • 위 식에 이미 상태의 분포 값이 들어가 있기에, MSE 값과 연관이 있다고 할 수 있음.
    • $\mu (s)$ 에 대해
      • 종종 $\mu (s)$ 는 상태 $s$ 에서 보낸 시간의 비율값이 선택됨.
      • on-policy 학습에서 이는 on-policy distribution(분포) 라고 하며, 이 장에서는 이 케이스에 초점을 맞춤
      • Continuing tasks 에서 on-policy distribution 은 $\pi$ 아래에서 정상성 분포이다.
        • 정상성 분포를 가진다고 가정하는 것.
        • 에피소드에서 무한한 상태를 수집할 수는 없으니, 일정 정도를 수집하여 분포를 구하고 이 분포가 정상 분포인 것을 가정하는 것이다.

    • The on-policy distribution in episodic tasks

      9_2_2_on_policy_distribution

      • 에피소드 작업에서 on-policy distribution 은 에피소드의 초기 상태가 선택되는 방식에 따라 약간 다르다.
      • $\eta(s) = h(s) + \sum_{\bar{s}} \eta(\bar{s}) \sum_a \pi (a | \bar{s} ) p(s | \bar{s},a)$, for all $s \in S$. (9.2)
        • $h(s)$ : 각 상태 s 가 첫 에피소드 시작일 확률
        • $\eta(s)$ : 에피소드에서 상태 $s$ 에 머무는 비율 (s에 방문하는 time step 수)
        • 에피소드가 $s$ 에서 시작하거나 이전 상태 $\bar{s}$ 에서 $s$ 로 전이가 일어난 경우
        • 위 식은 이전 상태의 time-step 비율을 이용해 현 상태의 비율을 구하는 식이다.
      • $\eta(s)$ 를 정규화 (on-policy distribution)
        • $\mu(s) = \frac{\eta(s)}{\sum_{s’} \eta(s’)}$, for all $s \in S$. (9.3)
          • $s’$ : 상태 $s$ 를 포함한 다른 모든 상태를 의미
        • 이것은 할인이 없는 경우에 대한 것임.
          • 할인이 있는 경우 9.2의 식의 두번째 항에 $\gamma$ 를 적용해야 함.
          • 여기에서 할인의 역할은 에피소드의 확률적인 시작과 종료를 다루기위한 요소로 사용되는 것임.
    • 연속적인 케이스와 에피소드 케이스 두 가지의 경우 비슷하게 동작하나, 근사하는 경우 완전히 분리해서 생각해야 한다. (향후 언급)
    • 위의 $\overline{VE}$ 로 학습목표 지정이 완료
      • 그러나 $\overline{VE}$ 가 강화학습에 적합한 성능의 목표인지 명확하지 않음.
      • 가치함수를 학습하는 궁극적인 이유는 더 나은 정책을 찾는 것임.
        • 이 목적을 위한 최고의 가치함수가 반드시 $\overline{VE}$ 를 최소화하는데 최적인 것은 아님.
      • 지금은 $\overline{VE}$ 에 중점을 둔다.
    • $\overline{VE}$ 학습목표의 이상적인 목표와 현실적 목표
      • 이상적인 목표 : 가능한 모든 $\textbf{w}$ 에 대해 $\overline{VE}(w^{*}) \leq \overline{VE}(w)$ 인 전역 최적의 가중치 벡터 $\textbf{w*}$ 를 찾는 것
      • 위 목표를 찾는 것은 선형과 같은 간단한 함수 근사에서는 가능하나, 인공신경망이나 의사결정트리와 같은 복잡한 함수근사에서는 거의 불가능하다.
        • 복잡한 함수근사에서는 이에 미치지 못하는, 지역 최적, $\textbf{w*}$ 와 유사한 수렴값을 찾게 된다.
        • 즉, 모든 상태에 대해 오차를 구해 합한 값 $\overline{VE}$ 의 변수 $\textbf{w}$ 에 대해, 전역최소값을 가지는 $\textbf{w}$ 는 구하기 힘들다는 이야기이다.
      • 이러한 수렴의 보장은 약간만 안심할 수 있지만, 일반적으로 비선형 함수 근사의 가능한 최선으로 여겨지고, 대부분의 경우 이정도로 충분하다.
        • 강화학습의 관심있는 많은 케이스의 경우 최적에 대한 수렴을 보장하지 않고, 또한 최적치에 대한 지정된 범위 내의 수렴 또한 보장하지 않는다.
        • 어떠한 방법의 경우 $\overline{VE}$ 로의 무한한 접근이 한계치를 넘어 발산하기도 한다.
    • 마지막 두 섹션은 광범위한 가치 추정을 위한 강화학습 방법에 광범위한 함수 근사 방법을 결합하는 프레임워크이다.
      • 전자의 업데이트를 사용하여 후자에 대한 훈련 예제를 생성한다.
      • 또한 $\overline{VE}$ 성능 측정을 통한 최소화의 촉진에 대해서 살펴본다.
      • 가능한 함수 근사 방식의 범위는 모두 다루기에 광범위하며, 대부분의 경우 신뢰할 수 있는 평가나 권장사항을 만들기에 알려진 정보가 너무 적다.
        • 우리는 몇 가지 가능성에 대해서만 살펴본다.
      • 이 챕터의 나머지 부분에서 경사 원리를 기본으로 한 함수 근사 방법에 집중하며, 이 중에서도 선형 경사 하강법에 중점을 둔다.
        • 우리는 이러한 방법이 특히 유망하다고 생각하며, 핵심적인 이론적 문제를 드러낸다고 생각한다. (또한 단순하기도 하다.)
  • Stochastic-gradient and Semi-gradient Methods
    • Stochastic Gradient Descent (SGD) : 확률적 경사하강법
      • 모든 함수 근사화 방법 중 가장 널리 사용되는 방법으로 온라인 강화 학습에 특히 적합함
      • 확률적이라는 뜻은, 모든 표본을 구해 경사하강법을 진행하는 것이 아닌, 일부 표본 데이터(상태)에 대해서만 적용한다는 의미임.
      • 경사 하강법에서 가중치 벡터는 고정된 실수 값을 구성요소로 가진 열 벡터이다.
        • $\textbf{w} \doteq (w_1, w_2, …, w_d)^\top$
          • 여기서 $\top$ 는 전치행렬을 의미한다. 수평의 row 벡터를 수직의 column 벡터로 전환하는 것을 의미
      • 근사가치함수 $\hat{v} (s, \textbf{w} )$ 는 모든 $s \in S$ 에 대한 $\textbf{w}$ 의 미분 가능한 함수이다.
      • 우리는 $\textbf{w}$ 를 매 이산 time-step 의 시리즈 $t = 0,1,2,3,…$ 각각에 업데이트를 할 것이므로, $\textbf{w}_t$ 라는 표기법이 필요하다.
      • 지금부터 우리는 각 스텝에서 새 예시 $S_t \mapsto v_\pi (S_t)$ (아마도 무작위로 선택된 $S_t$ 와 정책 하의 참 값) 를 관측한다고 가정한다.
        • 위의 상태 값은 환경과의 상호작용을 통한 연속적인 상태가 되겠지만, 여기에서는 그렇게 가정하지 않는다.
      • 비록 각 상태 $S_t$ 에 정확하게 옳은 참 값 $v_\pi (S_t)$ 이 제공된다 해도 여전히 어려운 문제가 있다.
        • 우리의 함수 근사기는 한정된 자원과 그로 인한 한정된 해결책을 가지고 있다.
        • 특히 일반적으로 모든 상태를 가지거나, 정확히 옳은 샘플들을 가지는 $\textbf{w}$ 는 존재하지 않는다.
        • 추가적으로 우리는 예제에 보여지지 않은 다른 모든 상태에 대해서도 일반화를 해야 한다.
      • 우리는 (9.1) 에 주어진 $\overline{VE}$ 를 최소화 하는동안 각각의 상태가 동일 분포 $\mu$ 로 나타난다고 가정한다.
        • 이러한 케이스에서 좋은 전략은 관측된 예제에서 에러값을 최소화하는 것을 시도해보는 것이다.

      • 확률적 경사 하강법 (SGD, Stochastic Gradient Descent) 은 각 예제 후에 해당 예제에서의 에러를 가장 많이 줄이는 방향으로 가중치 벡터를 소량 조정함으로서 위 방법을 수행한다.

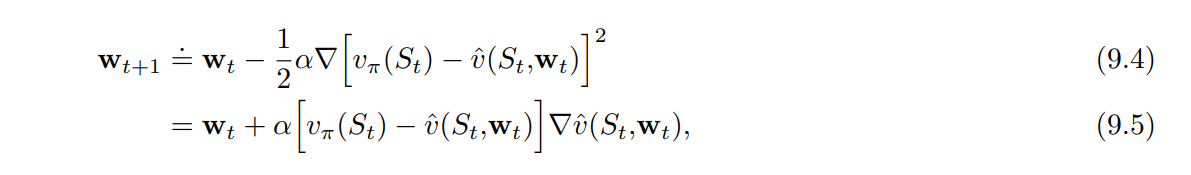
        9_3_1_sgd_vector_adjust_1

        • $\alpha$ : 양수의 step-size 파라미터
        • $w_{t+1} \doteq w_t - \frac{1}{2} \alpha \nabla [ v_\pi(S_t) - \hat{v}(S_t, w_t) ]^2$
          • $v_\pi (S_t)$ : 상태 $S_t$ 에서의 실 가치값
          • $\hat{v} (S_t, w_t)$ : 함수 근사를 통해 예측된 가치
          • 손실함수 $\textbf{L}$
            • $\frac{1}{2} [ v_\pi(S_t) - \hat{v}(S_t, w_t) ]^2$
            • 분산 : 편차의 제곱 평균
          • 즉, 위 식은 가중치 벡터를 학습률을 반영한 손실함수의 경사만큼 뺀 값
            • 손실함수의 값을 최소화 하는 방향으로 이동 (기울기의 반대방향)
          • 즉, 위 식에서 구하고자 하는 값은 $w_t -\alpha \nabla \textbf{L}$ 이 된다.
        • $= w_t + \alpha [ v_\pi (S_t) - \hat{v} (S_t, w_t) ] \nabla \hat{v} (S_t, w_t)$
          • 위 식 중 $\nabla \textbf{L}$ 을 구한다는 것의 의미는 손실함수에 대한 $w_t$ 의 기울기 함수를 구한다는 의미 (편미분)
          • $\textbf{L}$ 은 $v_\pi (S_t)$ 와 $\hat{v}(S_t,w_t)$ 의 함수이고, 후자는 $w_t$ 에 의존한다.
          • $\frac{\partial L}{\partial w_t} = \frac{\partial L}{\partial \hat{v}(S_t,w_t)} \cdot \frac{\partial \hat{v}(S_t,w_t)}{\partial w_t}$
          • 각 항에 대한 미분
            • $\frac{\partial L}{\partial \hat{v}(S_t,w_t)} = 2 \cdot \frac{1}{2} [ v_\pi (S_t) - \hat{v}(S_t,w_t) ] \cdot (-1) = \hat{v}(S_t,w_t)-v_\pi (S_t)$
            • $\frac{\partial \hat{v}(S_t,w_t)}{\partial w_t}$
          • 즉, $[ \hat{v} (S_t, w_t) - v_\pi (S_t) ] \nabla \hat{v} (S_t, w_t)$ 이 된다.

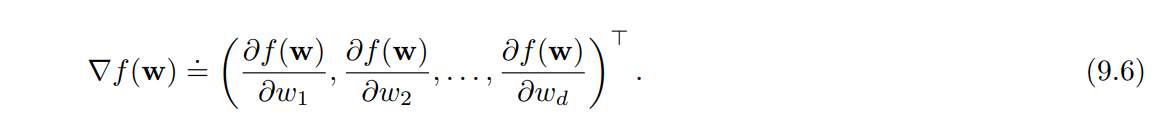
        9_3_2_sgd_vector_adjust_2

        • $f( \textbf{w} )$ : 벡터 w 의 함수.
        • $\nabla f( \textbf{w} )$ : 벡터의 구성요소에 대한 편미분
          • 위 식은 벡터 $\textbf{w}$ 에 대한 함수 $f( \textbf{w} )$ 를 미분하려면 벡터의 구성요소들로 편미분 해야 함을 나타낸다.
        • 이 파생 벡터는 $\textbf{w}$ 에 대한 $f$ 의 경사이다.
      • SGD 방식은 경사 하강 (gradient descent) 방식이라 하는데, $w_t$ 의 전반적인 단계가 예시의 제곱 에러 (9.4) 의 음의 기울기 값에 비례하기 때문
        • 이는 오차가 가장 빠르게 감소하는 방향이다.
      • 확률적으로 선택되었을 수 있는 단일 예에서 업데이트가 완료되면 경사 하강법을 확률적이라고 한다.
        • 많은 예를 통해 작은 단계만큼 수행하다 보면, 전반적인 효과는 $\overline{VE}$ 와 같은 평균 측정값을 최소화할 수 있다.
        • 한번에 큰 단계로 움직이거나 경사 방향으로 완전히 이동해 해당 예시에서의 에러를 완전히 없앨 수는 없다.
          • 모든 상태에 대해 에러가 없을 수 없고, 각각의 다른 상태에서 오직 에러의 균형을 근사화할 수밖에 없기 때문.
        • $\alpha$ 의 값이 충분히 작다면, SGD 방식은 지역 최적값으로 수렴하는 것을 보장한다.

    • Stochastic Gradient Descent (SGD) 의 Bootstrapping 개념에 대해

      • t 번째 학습 예제의 목표값을 $U_t \in \mathbb{R}$ 로 정의하면, $S_t \mapsto U_t$ 가 되며, 이때 $v_\pi (S_t)$ 의 참 값은 될 수 없지만, 임의의 근사치일 수는 있다.
        • 예를 들어 $U_t$ 는 $v_\pi (S_t)$ 의 노이즈 버전일 수 있고, 혹은 $\hat{v}$ 의 부트스트래핑된 목표일 수 있다.
        • 우리는 이 경우 (9.5) 의 정확한 업데이트를 수행할 수 없으나, $v_\pi (S_t)$ 를 $U_t$ 로 대체함으로써 근사 업데이트를 진행할 수 있다.

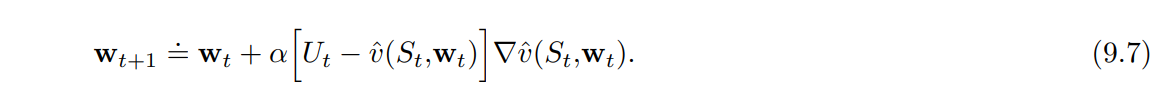
        9_3_3_sgd_u_t_update

        • 만약 $U_t$ 가 편향되지 않은 추정값이라면, 만약 각각의 $t$ 에 $\mathbb{E} [U_t | S_t=s ] = v_\pi (S_t)$ 라면 $w_t$ 는 지역 최적에 수렴함을 보장한다. ($\alpha$ 가 충분히 작을 경우)
          • 예를 들어 예시의 상태가 정책 $\pi$ 하에 환경과 상호작용 (혹은 시뮬레이션) 된 것이라면, 상태의 참 값의 정의는 리턴 값의 추측 값이기에, 몬테카를로 목표 $U_t \doteq G_t$ 는 편향이 없는 $v_\pi (S_t)$ 의 추정치이다.
        • 따라서 몬테카를로 상태값 예측의 경사하강법 버전은 국소적으로 최적의 솔루션을 찾는 것이 보장된다.

      • gradient monte carlo algorithm 의 psuedo code

        9_3_4_gradient_monte_carlo_algorithm_psuedo_code

        • $\hat{v} : S \times \mathbb{R}^d \to \mathbb{R}$
          • $S$ : 상태 공간을 의미
          • $\mathbb{R}^d$ : 실수의 $d$ 차원 벡터 공간을 의미
          • $\mathbb{R}$ : 실수를 의미
          • 따라서 $\hat{v}$ 함수는 상태 $s \in S$ 와 실수 벡터 $w \in \mathbb{R}^d$ 의 입력을 받아 실수를 출력한다는 의미이다.
      • Semi-gradient (bootstrapping) methods
        • $v_\pi (S_t)$ 의 부트스트래핑 추정 (9.7) 에서 목표가 $U_t$ 로 사용되는 경우 동일한 보장을 얻지 못한다.
          • 부트스트래핑 목표 n-step 반환값 $G_{t:t+n}$ 또는 DP 목표 $\sum_{a,s’,r} \pi (a|S_t) p(s’,r | S_t,a) [ r+\gamma \hat{v} (s’,w_t) ]$ 모두 가중치 벡터 $w_t$ 의 현재 값에 따라 달라짐. 이는 해당 대상이 편향될 것이며 실제 경사하강법을 생성하지 않음을 의미
          • 이는 (9.4), (9.5) 의 식에서 주요 단계가 $w_t$ 와 독립적인 대상에 의존하는 것에서 알 수 있음.
          • 따라서 $v_\pi (S_t)$ 대신 부트스트래핑 추정이 사용된 경우 이 단계는 유효하지 않게 됨.
          • 가중치 벡터 $w_t$ 를 변경하면 추정치에 미치는 영향을 고려하지만, 목표에 미치는 영향은 무시함.
        • 따라서 부트스트래핑 방법은 실제로 진정한 경사하강법 사례가 아니며, 경사의 일부만 포함되므로 Semi-gradient 방법이라고 한다.
      • Semi-gradient (bootstrapping) methods 의 장점
        • Semi-gradient (bootstrapping) 방법은 gradient 방법만큼 견고하게 수렴하지는 않지만, 다음 섹션에서 설명하는 선형 사례와 같은 중요한 경우 안정적으로 수렴한다.
        • 6장과 7장에서 살펴본 것처럼 일반적으로 훨씬 더 빠른 학습을 가능하게 한다.
        • 에피소드가 끝날 때까지 기다리지 않고도 학습이 지속적이고 온라인으로 이루어질 수 있다.
      • Semi-gradient TD(0) 의 psuedo code
        • 목표값 : $U_t \doteq R_{t+1} + \gamma \hat{v} (S_{t+1},w)$

        9_3_5_semi_gradient_td_0_psuedo_code

    • State Aggregation (Chat GPT 검색내용)
      • 강화학습에서 Function Approximation을 사용하는 방법 중 하나로 “State Aggregation”이라는 기법이 있다.
        • 이 방법은 상태 공간(state space)을 더 작은 그룹으로 나누는 것을 의미
        • 각 그룹은 하나의 상태로 취급되며, 이 방법은 연속적인 상태 공간을 이산적으로 변환하여 함수 근사를 적용할 때 유용
      • 주요 특징과 원리
        • 상태 그룹화 (State Aggregation): State Aggregation은 상태 공간을 작은 그룹 또는 상태 집합으로 나누는 프로세스. 연속적인 상태를 몇 가지 이산적인 상태로 집계하는 것과 유사
        • 상태 유사성: 유사한 특성 또는 관찰을 갖는 상태들이 동일한 그룹으로 집계. 이러한 유사성은 도메인 지식 또는 경험에 근거하여 결정
        • 함수 근사 적용: 이제 상태 그룹화를 통해 작은 상태 집합을 얻었으므로, 각 그룹에 대한 가치 함수를 추정할 수 있음.
          • Function Approximation 기법 중 하나인 선형 함수 근사(linear function approximation) 또는 비선형 함수 근사를 사용하여 각 그룹의 가치 함수를 근사
        • 업데이트 규칙: 상태 그룹화를 사용하면 상태 공간이 단순화되므로 각 그룹의 가치 함수 업데이트가 빨라질 수 있음. 에이전트는 각 상태 그룹의 가치 함수를 개별적으로 업데이트함.
        • 함수 근사 오류: 그러나 이런 단순화는 정보 손실을 의미하기도 한다. 각 상태 그룹 내에서 상태의 차이나 다양성을 잃을 수 있음. 따라서, State Aggregation을 사용할 때 어떤 정보 손실이 발생할 수 있음을 염두에 두어야 한다.
      • 주의점
        • State Aggregation은 강화학습에서 상태 공간이 커서 함수 근사를 적용하기 어려운 경우 유용한 방법 중 하나이다.
        • 그러나 주의해야 할 점은 그룹화 과정에서 상태 유사성을 올바르게 판단하고, 정보 손실을 최소화하도록 설계해야 한다는 것이다.
    • 예제 9.1: State Aggregation on the 1000-state Random Walk
      • 문제의 가정
        • 1000 개의 상태를 가진 random walk (예제 6.2, 예제 7.1 참고) 문제를 가정한다.
        • 상태 : 왼쪽에서 오른쪽으로 1 부터 1000까지 넘버링된 상태, 모든 에피소드는 중앙 (상태 500) 에서 시작
        • 상태 전이 : 현 상태 값에서 좌측 100 개, 우측 100개의 상태 내의 값 (전이 확률은 모두 동일)
        • 현 상태가 끝쪽에 가깝다면, 100 개의 이웃 상태보다 더 적은 상태가 있을 것이고, 이 경우 종료 상태에 확률이 합산된다.
          • 상태 1에서 왼쪽으로 이동해 종료될 확률 (상태 0) : 0.5
          • 상태 950 에서 오른쪽이로 이동해 종료될 확률 (상태 1001) : 0.25
        • 왼쪽 상태 (0) 에서 끝날 경우 보상은 -1, 오른쪽 상태 (1001) 에서 끝날 경우 보상 +1, 기타 다른 상태에서의 보상은 0

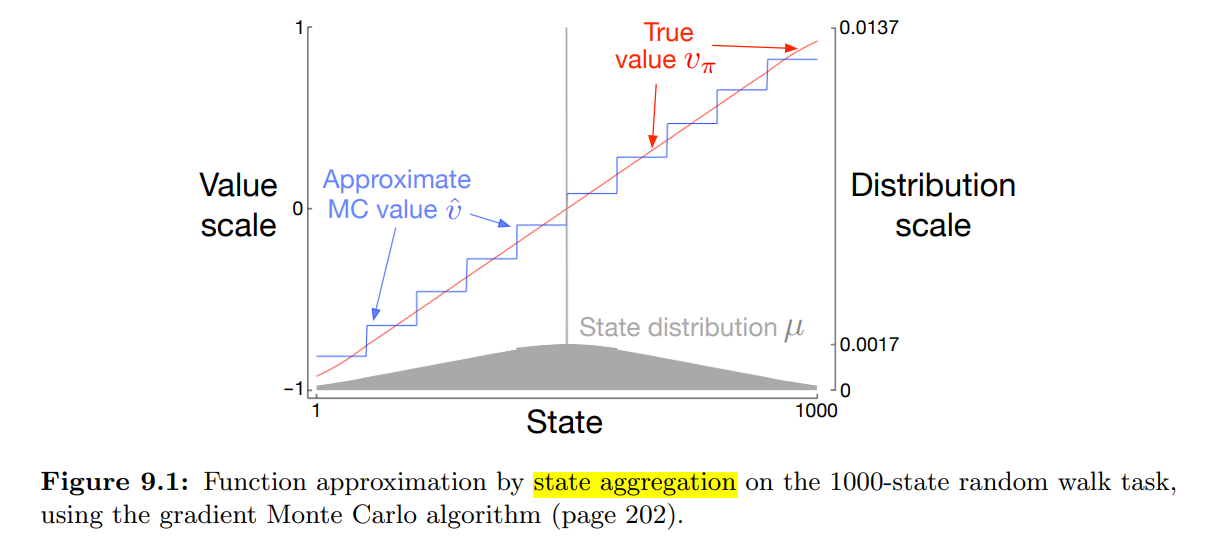
      9_3_6_figure_9_1_1000_state_random_walk_state_aggregation

      • 결과의 해석
        • Figure 9.1 은 이 작업의 참 가치 함수 $v_\pi$ 를 보여준다.
          • 이것은 거의 직선이지만, 종료상태 옆 마지막 100 개의 상태에서 수평으로 굽는 형상이다.
        • 또한 state aggregation 을 한, gradient Monte-Carlo 알고리즘을 통한 최종 근사 가치함수를 보여준다.
          • 100000 에피소드, step size $\alpha = 2 \times 10^{-5}$
          • state aggregation 은 1000 개의 상태에서 100개의 상태 묶음 10개 그룹으로 진행 (1-100, 101-200, …)
        • 계단 형태의 결과는 전형적인 state aggregation 의 효과이다.
          • 각 그룹에서 근사 가치는 상수이며, 하나의 그룹에서 다음 그룹으로 이동 시 이 상수 값이 급격히 변한다.
          • 이 근사 값은 $\overline{VE}$ 의 전역 최소값 (9.1) 과 가깝다.
        • 근사값의 일부는 상태 분포 $\mu$ 에 영향을 받게 된다.
          • 예를 들어 가장 극단의 값 (1) 보다 가장 왼쪽 그룹 중 상태 (100) 이 3배 이상 더 강한 가중치가 부여된다.
          • 따라서 그룹에 대한 추정치는 상태 (1) 의 참 값보다 상태 (100) 의 참 값 쪽으로 편향되게 된다.
  • Linear Methods
    • 가치함수가 가중치에 대해 선형인 경우
      • 함수 근사의 가장 중요한 특수 사례 중 하나는 근사함수 $\hat{v} (\cdot , \textbf{w} )$ 가 가중치 벡터 $\textbf{w}$ 에 대해 선형함수인 경우이다.
      • 모든 상태에 대응하는, $\textbf{w}$ 와 동일한 수의 구성요소를 가진, 실수 값 벡터 $\textbf{x} (s) \doteq (x_1(s), x_2(s), …, x_d(s))^\top$ 가 있다.
      • 이때, 선형 근사 상태-가치 함수는 $\textbf{w}$ 와 $\textbf{x} (s)$ 의 내적으로 구한다.

      9_4_1_linear_approximate_inner_product_between_w_and_x

      • 이러한 경우, 근사가치함수는 가중치에 대해 선형이다, 혹은 선형이다 라고 표현한다.
    • feature vector
      • 벡터 $\textbf{x} (s)$ 는 상태 s의 feature vector 라 한다.
        • $\textbf{x} (s)$ 의 각각의 구성요소 $x_i (s)$ 는 $x_i : \mathcal{S} \to \mathbb{R}$ 이다.
      • 선형 방법에서 feature 는 근사함수 세트에서 선형 기반을 형성하므로, basis function (기저함수) 가 된다.
        • 즉, 각각의 feature 가 각각의 차원을 이룬다.
        • d-dimensional feature vector 를 생성하는 것은 d basis function 을 선택하는 것과 같다.
        • features 들은 많은 서로 다른 방식으로 정의되며, 우리는 다음 장에서 몇 가지 가능성에 대해 다룬다.
    • 선형 가치근사함수와 SGD
      • 선형 가치근사에서 SGD 업데이트를 사용하는 것은 자연스럽다.
        • $\nabla \hat{v}(s,\textbf{w}) = \textbf{x}(s)$
      • 이는 선형 근사 상태-가치 함수가 $\textbf{w}$ 와 $\textbf{x} (s)$ 의 내적으로 구하기 때문임.
      • 그러므로 선형 케이스의 경우 SGD 업데이트 (9.7) 가 간단한 형태로 바뀌게 된다.
        • $w_{t+1} \doteq w_t + \alpha [ U_t - \hat{v}(S_t,w_t) ] \textbf{x} (S_t)$
      • 매우 간단하기 때문에 선형 SGD 사례는 수학적 분석에 가장 유리한 사례 중 하나이다.
      • 모든 종류의 학습 시스템에 대한 거의 모든 유용한 수렴 결과는 선형(또는 더 간단한) 함수 근사 방법에 대한 것이다.
        • (이 주장은 선형 가치 함수 근사가 간단하면서도 많은 문제에서 효과적으로 동작한다는 아이디어를 강조한 것입니다. 하지만 모든 문제에 대해 선형 근사가 항상 최적인 것은 아닙니다. 일부 문제에서는 더 복잡한 함수 근사가 필요할 수 있습니다.)
      • 선형의 경우 단 하나의 최적값 (혹은 최적값의 한 세트) 만 있으므로 지역최적값이나 전역최적값에 수렴하는 것이 자동적으로 보장된다.
        • 즉, 근사함수가 선형인 경우 $\frac{1}{2} [ v_\pi(s) - \hat{v}(s,w) ]^2$ 오차 값이 볼록한 형태를 가지고 하나의 최적값이 존재하게 된다.
    • 선형 가치함수근사와 Gradient Monte Carlo 알고리즘의 경우
      • 예를 들어 이전 섹션에서 제시된 gradient Monte Carlo 알고리즘은 시간이 지남에 따라 $\alpha$ 가 감소하면 선형함수근사 하에 $\overline{VE}$ 의 전역최적으로 수렴한다.
    • 선형 가치함수근사와 semi-gradient TD(0) 알고리즘의 경우
      • 마찬가지로 앞서 다룬 semi-gradient TD(0) 도 선형함수근사 하에 수렴하나, SGD 의 일반적 결과와는 다르다.
        • 가중치 벡터는 전역최적이 아닌 지역최적에 수렴한다. (특히 연속적인 케이스에서 중요)

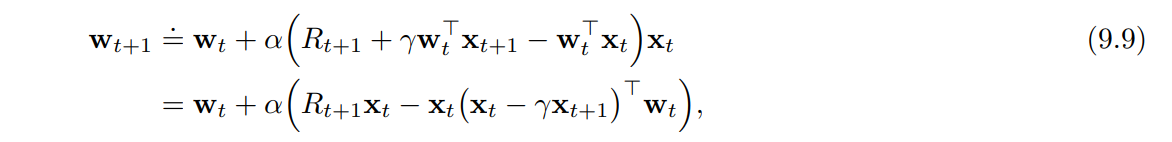
      9_4_2_update_semi_gradient_td_0

      • 여기에서 우리는 축약 표기 $\textbf{x}_t = \textbf{x}(S_t)$ 를 사용한다.
      • 시스템이 정상 상태에 도달하면 어떠한 $\textbf{w}_t$ 에 대해서도 다음 가중치 벡터를 아래와 같이 구할 수 있다.

      9_4_3_semi_gradient_td_0_td_fixed_point_1 9_4_4_semi_gradient_td_0_td_fixed_point_2

      • 위의 값을 TD fixed point 라고 한다.
        • 선형 semi-gradient TD(0) 는 이 지점으로 수렴한다.
      • 위 수식에 대한 이해 (Chat GPT 로 정리한 내 생각)
        • 즉 Semi-gradient 방식은 업데이트 식의 타겟에 학습 중인 가중치 벡터 $w$ 가 포함되어 수렴이 늦어지나
        • 근사함수가 선형일 경우 현재 목표 $w_{TD}$ 를 아래의 요소로 계산하여 구할 수 있으므로
          • $\textbf{x}_t$
          • $\textbf{x}_{t+1}$
          • $R_{t+1}$
        • 위 요소에 따라 $w_{TD}$ 의 값이 바뀔 수 있으나 학습해야 할 파라미터 $w$ 가 목표에 없으므로 더 빠르고 안정적인 수렴이 가능하다는 이야기.
      • Proof of Convergence of Linear TD(0)
        • 아래의 내용을 이해해보려 하였으나, 너무 복잡하여 본문 내용을 붙여넣는 것으로 갈음한다.

        9_4_5_proof_of_convergence_of_linear_td_0_1 9_4_5_proof_of_convergence_of_linear_td_0_2

        • 마지막으로, 이것은 TD(0) 알고리즘이 수렴할 때 가중치 벡터 $w_{TD}$ 에서의 에러가 전체 상태 공간에서의 최적 에러 $w^*$ 에서의 에러에 대한 한계로 나타나며, $\gamma$ 가 충분히 작을 때 $w_{TD}$ 의 에러가 최적 에러에 근접함을 보여준다.
          • $\overline{VE}(w_{TD}) \leq \frac{1}{1-\gamma} \min_w \overline{VE}(w)$

      • 가능한 가장 작은 에러 값에 대한 $\overline{VE}$ 의 경계치

        9_4_6_td_fixed_point_ve_error_bounded

        • Chat GPT 로 내가 확인한 내용
          • $w_{TD}$ 는 부트스트래핑으로 얻은 특정 상태에 대한 추정값으로, 실제 값과는 오차가 있을 수 있다.
          • $w$ 는 $w_{TD}$ 와는 별개로, 전체 상태에 대한 가중치 값을 학습하는 것으로, 각 상태의 $w_{TD}$ 로부터 추정된 값과 $w$ 로 계산된 값 사이의 오차 합을 최소화하려고 노력한다.
          • 부등식 $\overline{VE}(w_{TD}) \leq \frac{1}{1-\gamma} \min_w \overline{VE}(w)$ 는 $\gamma$ 값이 충분히 작을 때 $w_{TD}$ 의 각 상태에 대한 평균 에러가 전역최적 $w$ 의 평균 에러 값으로 계산된 경계 영역보다 작음을 보장한다는 내용이다.
        • 즉, TD 방법은 $\gamma$ 값이 1에 가까워지면, 점근 성능에 상당한 잠재적 손실이 있을 수 있으나, 종종 몬테카를로 방법에 비해 분산이 크게 줄어들어 더 빠르게 수렴할 수 있다.
        • 9.14 와 유사한 경계는 다른 정책 부트스트래핑 방법에도 작용되며, Sarsa(0) 와 같은 방법이나 에피소드 작업과 같은 방식도 유사한 경계값이 있음.
          • 보상, 기능, step-size 매개변수 감소에 대한 몇 가지 기술적 조건이 있으나 여기에서는 생략함.
        • 이러한 수렴 결과에서 중요한 것은 상태가 정책 분포에 따라 업데이트된다는 것이다.
          • 다른 업데이트 분포의 경우 함수 근사를 사용하는 부트스트래핑 방법은 무한대로 발산할 수 있다.
          • 이에 대한 예와 가능한 해결 방법은 11장에서 다룬다.
    • 예제 9.2 : Bootstrapping on the 1000-state Random Walk
      • 이 장에서 관찰한 내용 중 일부를 설명하기 위해 1000개 상태의 랜덤 워크의 예제를 사용 (State aggregation + 선형함수근사)

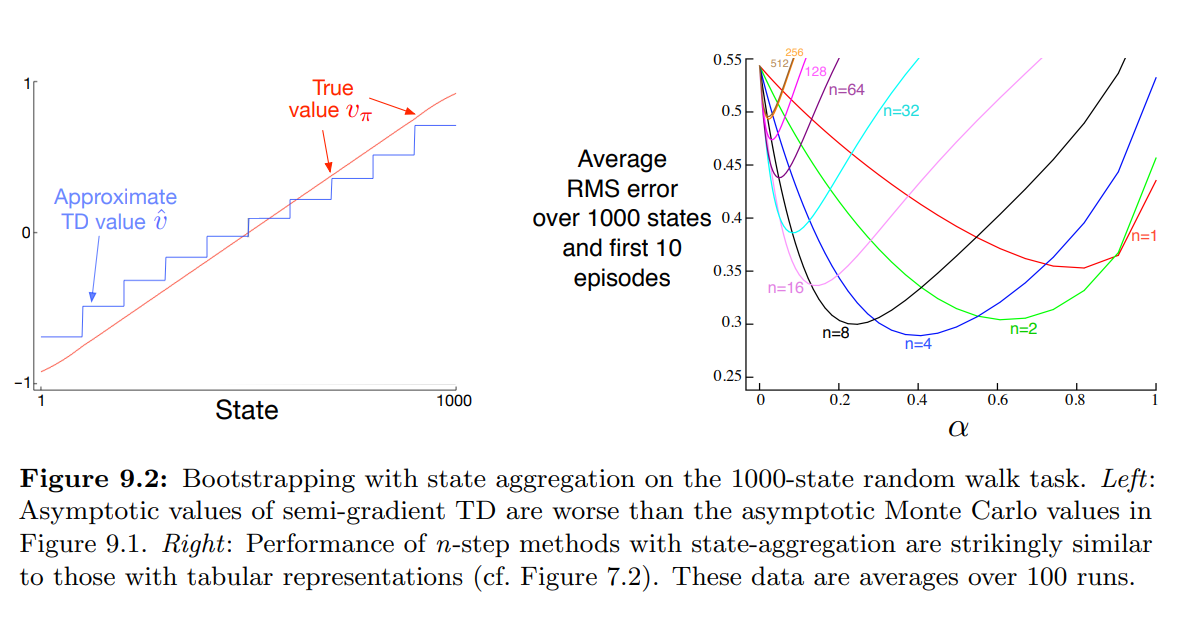
      9_4_7_figure_9_2_bootstrapping_with_state_aggregation_1000_step_random_walk_example_result

      • 왼쪽 패널은 예제 9.1 과 동일한 State aggregation 을 사용, Semi-gradient TD(0) 에 의한 학습된 최종 값 함수를 보여줌
        • TD 근사가 몬테카를로 근사보다 실제 값에서 더 멀다는 것을 알 수 있음
      • 오른쪽 패널은 그림 7.2 (n-step semi-gradient TD + state aggregation) 와 유사한 결과를 보여준다.
        • 함수근사를 한 것과, tabular 계산을 한 것의 유사성을 보여줌
      • semi-gradient n-step TD 알고리즘은 tabular n-step TD 알고리즘에서 semi-gradient 함수 근사를 확장한 것으로 psuedocode 는 아래와 같다.

      9_4_8_n_step_semi_gradient_TD_psuedo_code

      9_4_9_key_equation_n_step_semi_gradient_TD

Estimating Value Functions as Supervised Learning

Moving to Parameterized Functions

  • Tabular Methods
    • 모든 가능 상태를 표현하는 테이블 형태의 저장공간에 각각의 학습 값을 저장하는 형태
    • 하지만 실제 세계의 문제들의 경우 이 테이블 저장공간이 추적불가능할 정도로 커지게 된다.
      • 로봇이 카메라를 통해 세계를 관찰하는 경우, 모든 가능한 이미지를 저장할 수는 없음.
  • 학습목표
    • 파라미터화된 함수를 사용하여 근사값을 구하는 법 이해하기
    • 선형 가치함수근사의 의미를 설명하기
    • tabular 케이스 또한 선형 가치함수근사의 특별한 케이스임을 이해하기
    • 가치함수근사를 파라미터화 하는 많은 방법이 있음에 대해 이해하기

  • 다양한 형태로 표현가능한 가치 함수

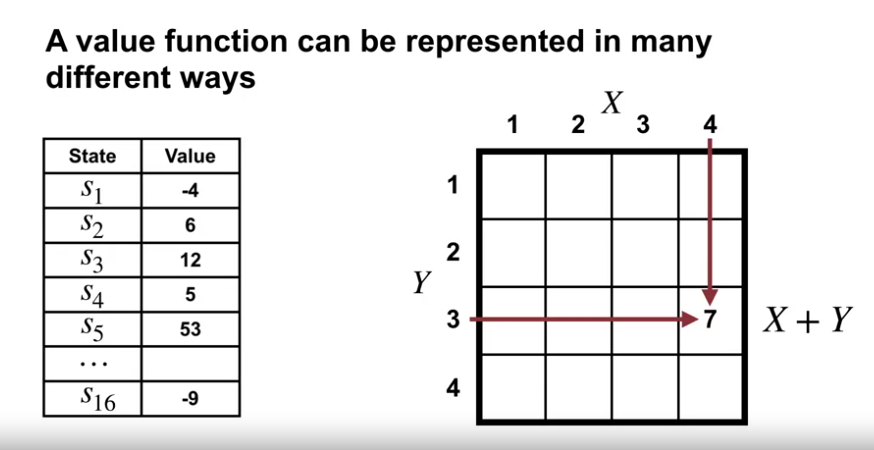
    value_function_tabular_and_linear_approximation

    • 좌측은 tabular 형태로 각각의 가치함수값을 가지고 있는 형태
      • 각각의 상태에 따라 독립된 값을 테이블에 저장하는 형태 (지금까지 학습한 방식)
      • 학습이 진행됨에 따라 테이블에 저장된 값을 업데이트한다.
    • 우측은 X 와 Y 좌표 값에 따라 X + Y 가치함수를 가진 형태
      • 이론적으로 우리는 상태를 제공받아 실수를 출력하는 어떠한 함수도 사용할 수 있다.
      • 하지만 이러한 형태를 가치함수로 사용하기를 원치 않음.
        • 이 예측치를 수정할 방법이 없음 (학습할 방법이 없음)
  • Parameterized function
    • $\hat{v}(s,\textbf{w}) \approx v_\pi (s)$
      • $\textbf{w}$ : weights (가중치) - 함수에 변화를 주기 위한 조정이 가능해짐.

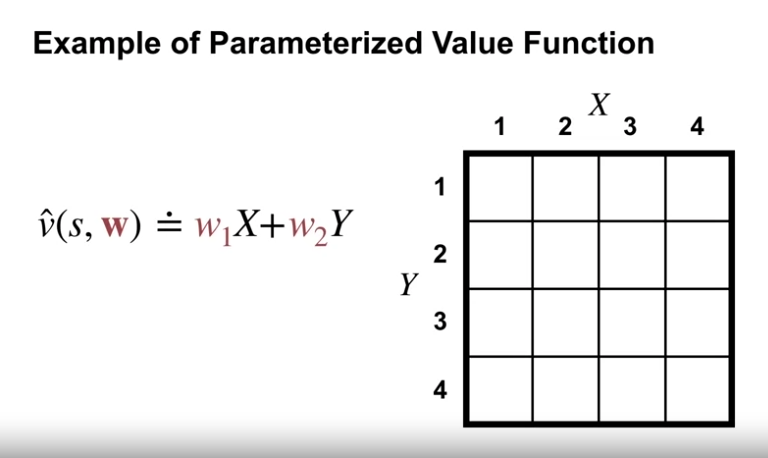
    example_parameterized_value_function

    • $\hat{v}$ : 참 가치함수 값을 근사하는 함수의 의미
    • $\textbf{w}$ : 함수근사에 대하여 모든 가중치를 파라미터화 한 벡터 값
    • 여기에서 우리는 모든 상태에 대한 가치함수 값을 저장하는 것이 아닌, 2개의 가중치만을 저장하게 된다.

  • 가중치(Weight) 의 변화가 가치함수에 주는 영향

    weight_impact_value_function

    • tabular case 의 경우 하나의 상태값에 영향을 주지만
    • Parameterized function 의 경우 가중치 하나를 변경할 경우 복수 개의 상태에 변화를 준다.

  • Linear Value Function Approximation

    linear_value_function_approximation

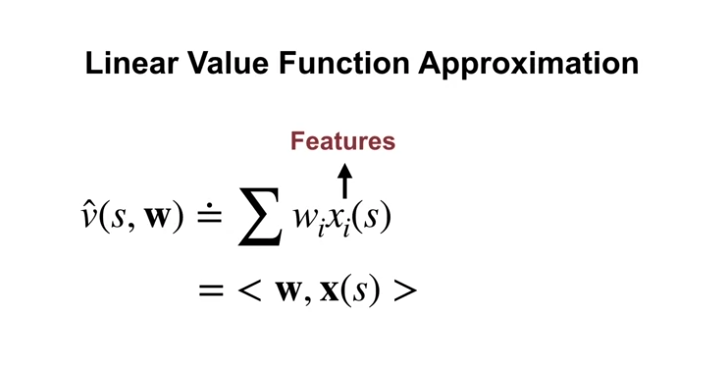
    • 가중치와 어떠한 고정된 속성 (feature) 간의 곱의 합
    • 위의 식일 간단하게 weight vector $\textbf{w}$ 와 feature vector $\textbf{x} (s)$ 간의 내적 (inner product) 으로 표현한다.

  • Limitations of Linear Value Function Approximation

    limitations_of_linear_value_function_approximation

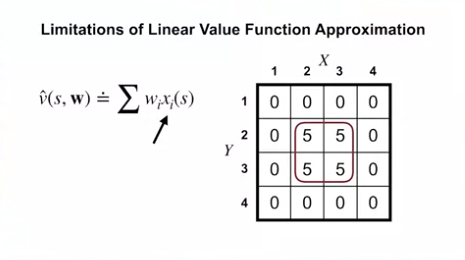
    • 위의 linear value function approximation 을 살펴보면 X, Y feature 에 대해서 선형적인 표현만 할 수 있다.
    • 만약 참 값이 위의 그림과 같다면 X, Y feature 에 대한 선형 함수로는 표현할 방법이 없다.
      • 외각의 0 을 표현하기 위해서는 $W_1$ 과 $W_2$ 가 0이 되어야만 한다.
      • 그렇게 된다면 내부의 5를 표현할 방법이 없다.
    • 그러나 우리가 반드시 X, Y 값을 features 로 사용할 필요는 없다.
      • 즉, Linear value function 은 좋은 특징(features) 값을 가지는 것이 중요하다.
        • 특징(features) 을 정의하는 데 다양한 효과적인 방법들이 있다.

  • Tabular case 를 linear function 으로 표현하는 방법

    tabular_value_function_is_linear

    • 각각의 상태를 feature 로 정의한다.
    • 이에 대응하는 가중치 값과의 내적을 구하면, 왼쪽의 Tabular case 와 동일한 연산이 된다.

  • Nonlinear Function Approximation

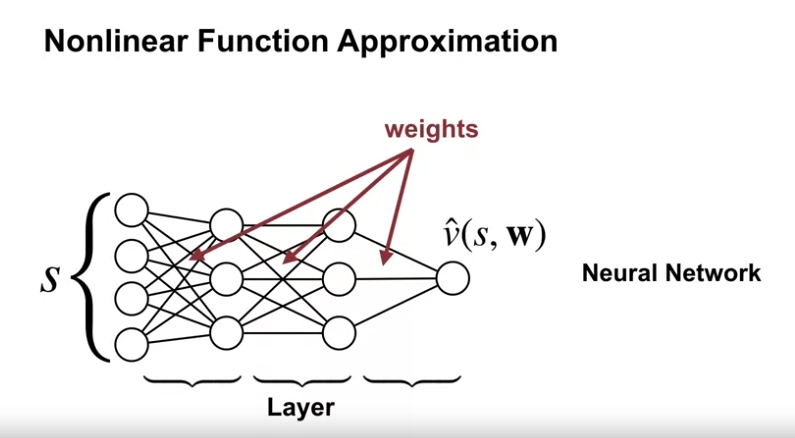
    nonlinear_function_approximation_NN

    • 신경망 방식 또한 비선형 가치근사 방법 중 하나이다.
    • 이 또한 parameterized function 중 하나이다.
    • 상태 S 가 실제 가중치 값들 $\textbf{w}$ 를 통과하며 $\hat{v}(s, \textbf{w})$ 의 연산을 하게 된다.

Generalization and Discrimination

  • Generalization 에 대해
    • 함수 근사에서 가장 중요한 고려사항은 어떻게 상태들을 일반화 (Generalize) 할 것인지 이다.
    • Generalization 의 예
      • 어떤 사람이 특정한 자동차를 운전하는 방법을 배울 경우, 다른 자동차의 운전 방법을 배울 때 처음부터 배우지 않는다.
      • 혹은 다른 도로에서 운전하거나, 비 오는 도로에서 운전한다고 처음부터 배우지 않는다.
  • 학습목표
    • generalization (일반화) 와 discrimination (차별) 의 의미 이해하기
    • generalization (일반화) 의 혜택 이해하기
    • 가치 근사에서 왜 generalization (일반화) 와 discrimination (차별) 모두가 필요한지 설명하기
  • Generalization
    • 직관적 의미 : 특정한 상황에서의 지식을 적용하여 광범위한 상황에서의 결론을 도출하는 것
    • 정책 평가에서의 의미 : 하나의 상태에서 추정값의 업데이트가 다른 상태의 값에도 영향을 주는 것

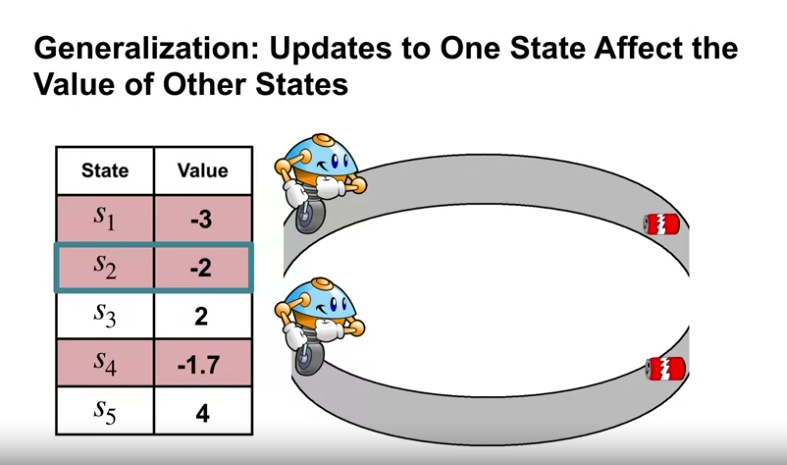
    generalization_updates_one_state_affect_other_state

    • 위의 그림처럼 가령 비슷한 시간이 소요되는, 비슷한 거리의 캔을 수거하러 가는 경우 센서에 의해 다른 값이 읽히더라도 비슷한 값이 도출될 수 있다.
      • 이러한 경우 위의 두 상태에 대해 가치함수의 일반화를 하길 원한다.
    • 일반화를 통해 더 빠른 학습의 진행이 가능하다. (아직 방문하지 않은 상태에 대해서도 업데이트가 가능함)
  • Discrimination
    • 두 개의 상태를 구분하여 두 개의 상태가 다르도록 만드는 능력

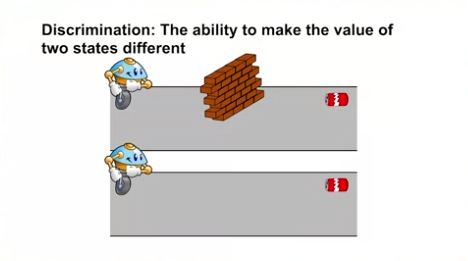
    discrimination_make_two_states_different

    • 거리가 같더라도 벽 뒤에 있는지, 벽이 없는지에 따라 상태를 구분해야 한다.
    • 따라서 비슷한 거리에 있는 캔에 대해 상태를 일반화하는 것도 중요하나, 다른 정보에 따라 상태를 구분하는 것도 중요하다.

  • 일반화와 구분에 따른 카테고리화

    • Tabular Methods : 구분은 뛰어나나 일반화는 전혀 못함. 각 상태에 대해 독립적인 학습을 진행함.
    • Aggregate All States : 모든 상태를 똑같은 상태로 판단. 상태에 대한 학습이 불가함
    • $*$ (●:현실적인 목표) : 좋은 구분과 좋은 일반화를 달성한 상태로, 비슷한 상태끼리 학습을 같이 진행하여 빠른 학습을 하고, 상태간 구분을 하여 정확히 근사를 하는 상태
      • 예를 들어 비슷한 상태그룹을 나타내는 feature 를 표기한다.

  • Generalize 방법에 대해

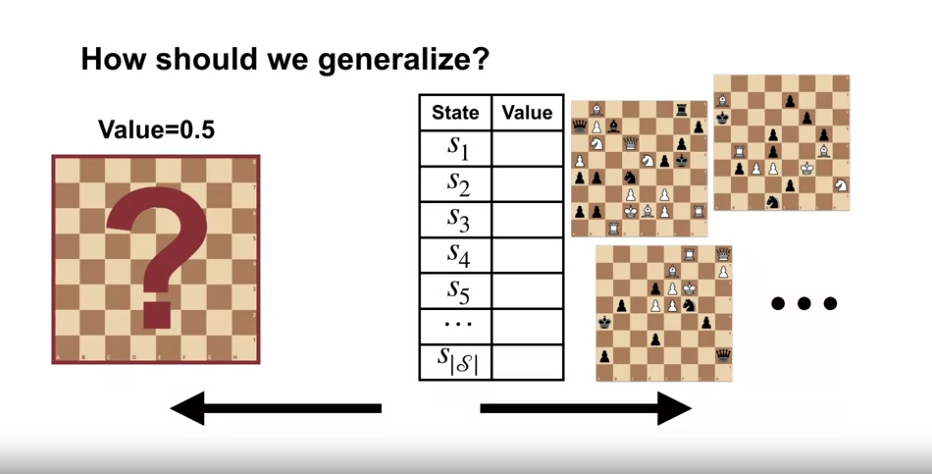
    generalize_chess_how

    • 좌측은 극단적인 Generalize 로 모든 체스게임 상태를 동일한 상태로 보고, 승률을 0.5 로 책정한 경우 (안좋은 예측값)
    • 우측은 Tabular Case 의 경우로 모든 경우의 수에 대해 승률을 책정한 경우 (경우의 수가 너무 많아 불가능)
    • 우리는 이 사이의 무언가를 원한다.
      • 비슷한 승률 (비슷한 상태) 끼리의 그룹화는 어려운 질문이다.
      • 이것은 우리의 알고리즘 성능에 지대한 영향을 미치며, 머신러닝과 강화학습의 중심 화제이다.

Framing Value Estimation as Supervised Learning

  • 학습목표
    • 어떻게 가치 측정이 지도학습 문제에 포함될 수 있는지 이해하기
    • 모든 가치근사방식이 강화학습에 잘 적용될 수 없다는 점을 식별하기

  • Supervised learning

    function_approximation_similarity_supervised_learning

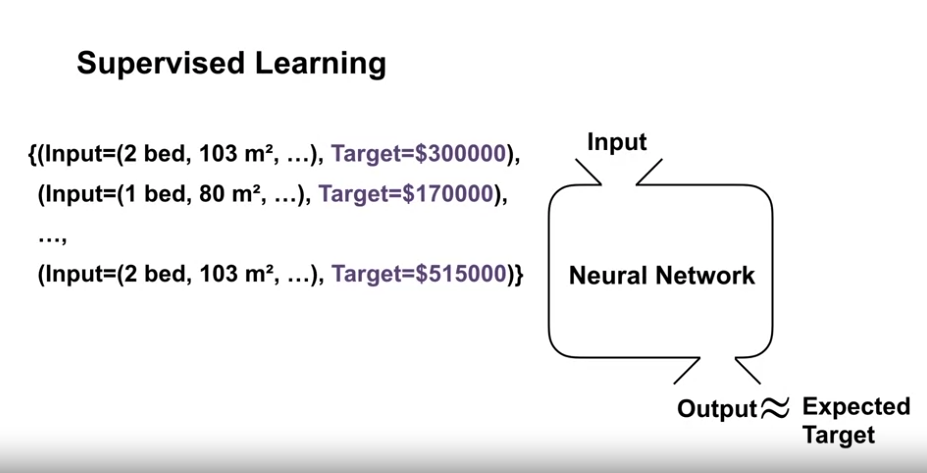
    • 지도학습도 입력 값과 목표 값을 이용해 함수를 근사시키는 과정은 동일하다.
    • 학습 세트에 없는 입력값에 대해서, 일반화를 통해 실 가치와 유사한 값을 얻길 원한다.
    • 이러한 parameterized function 은 여러 형태로 표현될 수 있는데, 그 중 하나가 신경망이다.

  • Monte Carlo 방식과 Supervised Learning 의 유사성

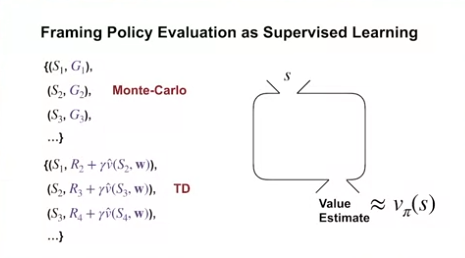
    function_approximation_similarity_MC

    • Policy Evaluation 에 있어서, Monte Carlo 는 샘플의 리턴값을 이용하여 가치 함수를 추정하는 방식이다.
      • 이 또한 입력값이 상태, 목표 값이 리턴 값인 지도학습의 일환으로 볼 수 있다.
      • 또한 모든 상태에서 함수가 참 값과 유사한 예측값을 출력하기를 원한다.
      • 이는 TD 또한 마찬가지이다.

  • 모든 가치근사 방식이 강화학습에 잘 적용될 수 없는 이유

    • 온라인 업데이트
      • 에이전트가 환경과 상호작용을 하면서 계속 새 데이터를 만드는 경우 (즉, 처음부터 전체데이터에 접근 가능한 Offline Learning 과 차이가 있음)
      • 함수 근사를 사용할 때, 해당 방식이 온라인 환경에서 잘 적용될 수 있는지를 생각해 봐야 한다.
      • 어떠한 근사 방법은 고정된 배치 데이터를 사용해야 하거나, 시간적으로 상관된 데이터 (강화학습은 언제나 상관되어 있다.) 에 맞지 않는 경우가 있다.
    • 부트스트래핑
      • 타겟 값이 현재의 추측값과 연관이 있을 경우
      • 계속적으로 타겟 값이 변동되는 경우

The Objective for On-policy Prediction

The Value Error Objective

  • 학습목표
    • 정책 평가를 위한 평균제곱오차 (mean squared value error) 의 목표 이해
    • 목표에서 상태 분포 (state distribution) 의 역할을 설명하기
  • An Idealized Scenario
    • 예를 들어 모든 상태에 대한 참 값을 알 수 있는 상태라고 가정하자.
      • ${(S_1, v_\pi(S_1)), (S_2, v_\pi(S_2)), (S_3, v_\pi(S_3)), …}$
    • 우리는 이 참 값과 최대한 유사한 값을 출력할 수 있는 근사 함수를 찾아야 한다.
      • $\hat{v}(s,\textbf{w}) \approx v_\pi(s)$
    • 하지만 위 근사함수가 모든 상태에서 참 값과 동일한 값을 출력할 수는 없다.
      • 우리는 가중치 $\textbf{w}$ 값을 조절하여 최대한 좋은 결과를 얻고자 한다.
      • 우리는 어떠한 측정치를 이용하여 우리의 예측을 보다 정확하게 조절할 필요가 있다.
  • The Mean Squared Value Error Objective
    • 문제의 가정
      • 선형 가치근사함수 $\hat{v}$
      • 상태는 1차원에 연속적이라고 가정

    mean_squared_value_error_objective

    • Squared Value Error
      • $[v_\pi(s) - \hat{v}(s, \textbf{w} )]^2$
      • 참 값과 추정 값 간의 오차를 측정할 수 있는 전통적인 방법
      • 문제는 하나의 상태에서 오차가 준다면, 다른 상태에서 오차가 늘어날 수도 있다는 점이다.
    • Sum of Squared Value Error
      • $\sum_s [v_\pi(s) - \hat{v}(s, \textbf{w}) ]^2$
      • 모든 상태에서의 오차 합을 측정
      • 하지만 과연 모든 상태가 서로 같은 중요도를 가진다고 볼 수 있을까?
    • Sum of Mean Squared Value Error
      • $\sum_s \mu(s) [v_\pi(s) - \hat{v}(s, \textbf{w}) ]^2$
      • $\mu(s)$ : 해당 정책 하에 s 상태에 방문한 빈도 수를 전체 빈도수 대비 분수로 나타낸 것
        • 많이 방문한 상태의 에러 값에 더 많이 집중하고, 드물게 방문한 상태의 에러값에 덜 신경 쓰는 것
        • 해당 값은 확률분포 값이다.
  • Adapting the Weights to Minimize the Mean Squared Value Error Objective
    • $\overline{VE} = \sum_s \mu(s) [v_\pi(s) - \hat{v}(s, \textbf{w})]^2$
    • 우리는 가중치 $\textbf{w}$ 를 조정하여 Mean Squared Value Error 값을 최대한 작게 만드는 것이 목적이다.
    • 이 Objective 를 VE bar 라고 한다.
    • 함수 근사를 이용한 정책의 평가는 특정한 목표값을 정의해야 한다.
    • Mean Squared Value Error 는 이러한 목표값 중 하나이다.

Introducing Gradient Descent

  • 학습목표
    • 경사하강법의 개념을 이해한다.
    • 경사하강법이 고정된 한 지점으로 수렴하는 것을 이해한다.

  • Recap : Learning Parameterized Value Functions

    recap_learning_parameterized_value_functions

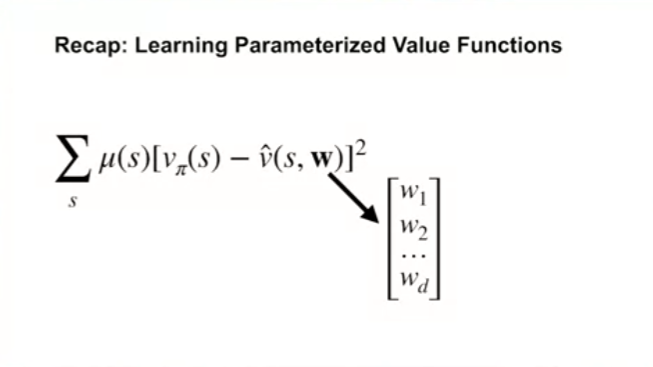
    • 가중치 $\textbf{w}$ 는 실제 실수 값들로 이루어져 있다.
    • 위의 연산을 보면, 가중치의 변화는 많은 상태에 영향을 줄 수 있다.
    • 우리의 목표는 전체 에러값 (Overall value error) 의 최소화이다.

  • Understanding Derivatives (미분 이해하기)

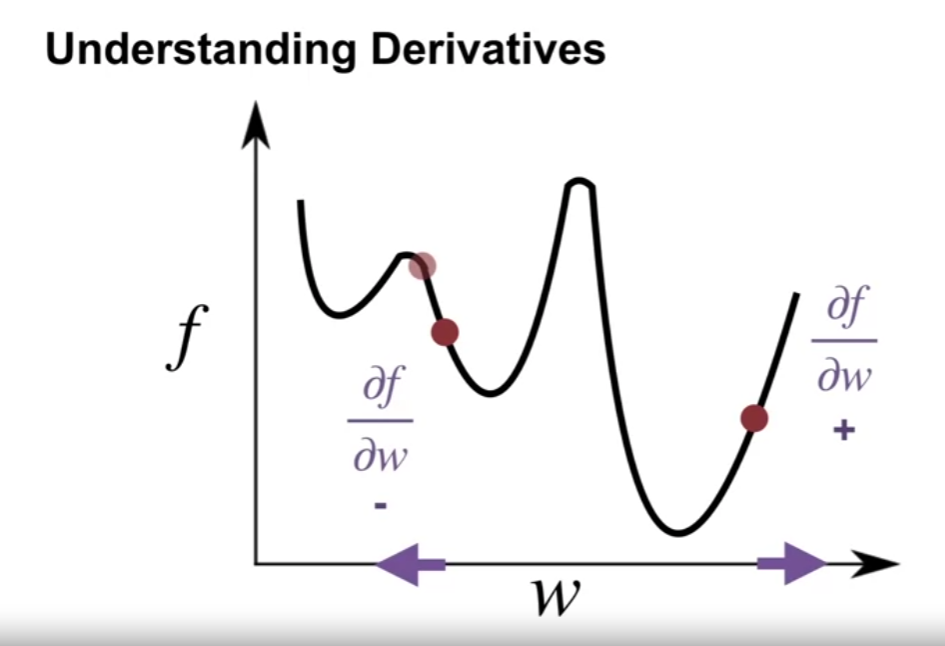
    understanding_derivatives

    • $f$ : function, 여기에서는 위 value error 로 이해
    • $W$ : 가중치의 스칼라 파라미터로 이해
    • 여기에서 미분 값으로 $W$ 값의 지역적 변화에 대해 $f$ 값을 증가시킬지 감소시킬지를 알 수 있다.
      • 미분 값의 음수, 양수의 여부로 $W$ 포인트에서 $f$ 증가, 감소에 대해 판단
      • 미분 값의 절대값 크기로 $W$ 포인트에서의 경사 (얼마나 급변하는지) 에 대해 판단
      • 여기에서 미분 값의 기울기 방향으로 $W$ 를 이동시키는 것은 $f$ 의 값을 증가시키는 방향으로 이동하는 것임

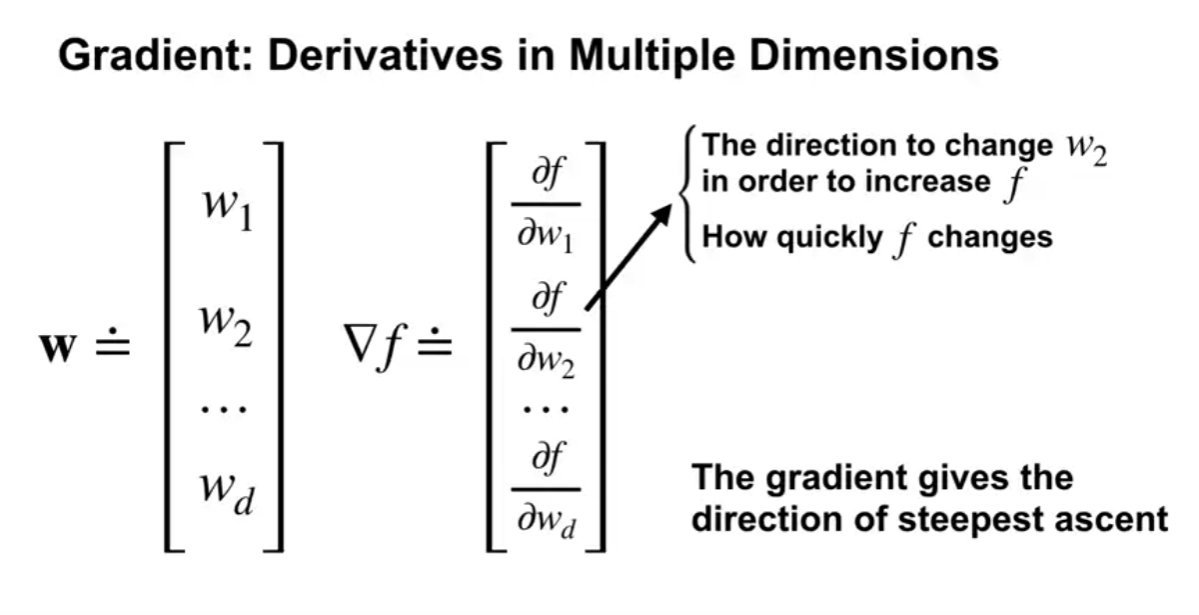
    gradient_derivatives_in_multiple_dimensions

    • $\textbf{w}$ 의 벡터 요소의 수 (차원) 에 따라 여러 차원의 미분값이 존재한다.
      • 이 각각의 차원들에 대해서도 위의 규칙이 통용된다.

  • Example : Gradient of a Linear Value Function

    example_gradient_of_a_linear_value_function_1

    • 이전에 다뤘듯, 선형가치근사함수에서의 가치함수값은 단순 가중치와 상태 feature vector의 내적이었다.
    • 이 때, feature vector 는 가중치와는 독립적인 값이므로, 미분 값이 해당 상태의 feature vector 그 자체가 되게 된다.

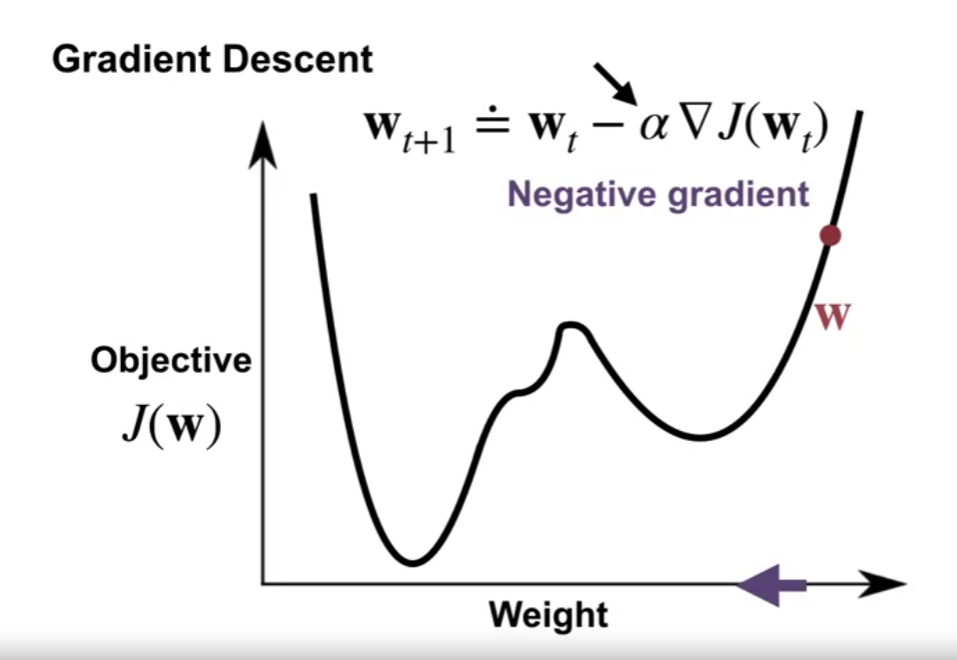
    example_gradient_of_a_linear_value_function_2

    • 목표 값은 $\textbf{w}$ 에 대한 함수이다.
      • $\hat{v}$ 가 $\textbf{w}$ 에 대한 함수이기 때문
      • 우리의 목표는 이 함수 값을 최소화 하는 것이다.
    • $\alpha$ : 얼마나 움직일지 (step-size) 를 정의. 미분 값은 지역적인 영역에서의 증감만을 보장하기 때문
    • 적은 양으로 가중치를 조절하다 보면 Gradient 값이 0이 되는 부분이 있는데 이 부분을 지역최소값 (local minumim) 이라 한다.
      • 해당 가중치 $\textbf{w}$ 가 당장의 근처 값보다 낫다는 것을 보여줌. (하지만 최적의 값은 아닐 수 있음)
  • Global Minima and Solution Quality
    • 전역최적값 (global minimum) $\textbf{w}_*$ 에서의 $\hat{v}$ 값이 반드시 참 값일 필요는 없음. (충족하지 않음)
      • $\hat{v} \ne v_\pi$
      • 이것은 function parameterization 의 한계이기도 하고, 목표값(objective)의 설정에도 영향을 받는다고 볼 수 있음
    • 만약 feature vector 값이 상태와 무관하게 언제나 1이라면, Mean Squared Value Error 목표값을 최소화 하는 근사가치함수 (모든 상태에 대해 평균 값을 제공) 를 찾을 수는 있겠지만 이것이 좋은 가치함수라고 볼 수는 없다. (이 경우는 feature vector 가 잘못 설정된 경우)

Gradient Monte for Policy Evaluation

  • 학습목표
    • 경사하강법과 확률적 경사하강법을 사용하여 오차값을 최소화 하는 방법 이해하기
    • 가치 추정을 위한 Gradient Monte Carlo 알고리즘의 이해

  • Gradient of the Mean Squared Value Error Objective

    gradient_of_the_mean_squared_value_error_objective

    • 첫번째로 목표값 (Objective) 의 Gradient 를 찾아야 한다.
      • 위의 경우 Mean Squared Value Error 의 Gradient 를 찾아야 한다.
      • Mean Squared Value Error : A weighted sum of the squared error over all states.

    from_gradient_descent_to_stochastic_gradient_descent_1

    • Mean Squared Value Error 에 대한 Gradient 를 계산하는 것은 모든 상태에 대한 합, 모든 상태의 확률분포에 대한 계산을 의미
      • 일반적으로 실현이 불가능하다.
      • 대부분의 경우 분포값 $\mu$ 를 알지 못한다.

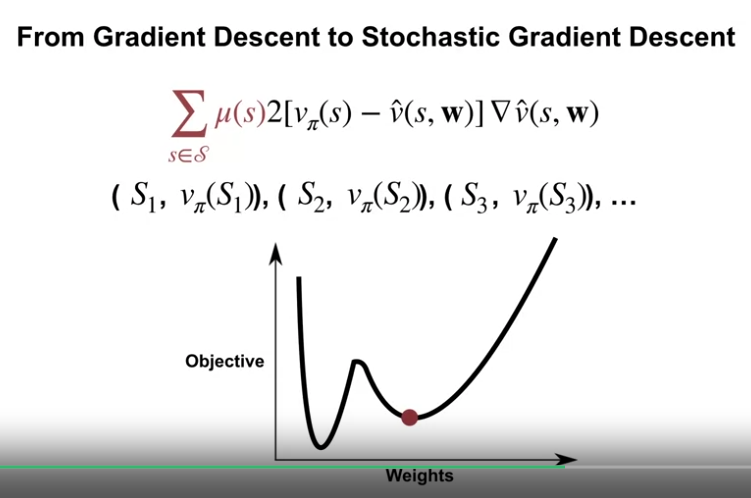
    from_gradient_descent_to_stochastic_gradient_descent_2

    • 이상적인 설정 - $v_\pi$ 에 접근이 가능한 경우
      • 명시적으로 $\mu$ 가 없더라도, 정책을 따름으로서 상태를 샘플링할 수 있다.
      • 정책을 따르면서 얻은 상태에 대한 가중치의 즉각적인 업데이트가 가능하다.
      • 하나의 차원으로 볼 때, 상태 샘플에 따라 에러값이 늘어날 수도 있지만 점진적으로 개선되어간다.
    • 위와 같은 업데이트 접근법을 확률적 경사하강법 (Stochastic Gradient Descent) 이라 한다.
      • 즉, 확률적이란 모든 상태에 대한 업데이트가 아닌, 정책을 따라 얻은 샘플링된 상태에 대한 업데이트를 한다는 뜻
      • 이 확률적 경사하강법은 경사에 대한 노이즈가 있는 근사라고 볼 수 있다.
        • 계산비용이 훨씬 저렴함
        • 최소값까지 꾸준한 발전을 이룰 수 있음

  • Gradient Monte Carlo

    gradient_monte_carlo

    • 위의 Stochastic Gradient Descent 에는 한계점이 있다.
      • 우리는 $v_\pi$ 에 접근할 수 없다.
      • 이 $v_\pi$ 값을 정책을 따라 얻은 리턴값으로 대체한다. (Monte Carlo 방식)
      • 생성된 에피소드 샘플에 대하여 가중치 업데이트를 진행한다.

State Aggregation with Monte Carlo

  • 학습목표
    • 가치함수의 근사를 위한 state aggregation (상태 집합) 기법 사용법 이해
    • state aggregation (상태 집합) 과 함께 Gradient Monte Carlo 방식 적용

  • Random Walk Example

    random_walk_example

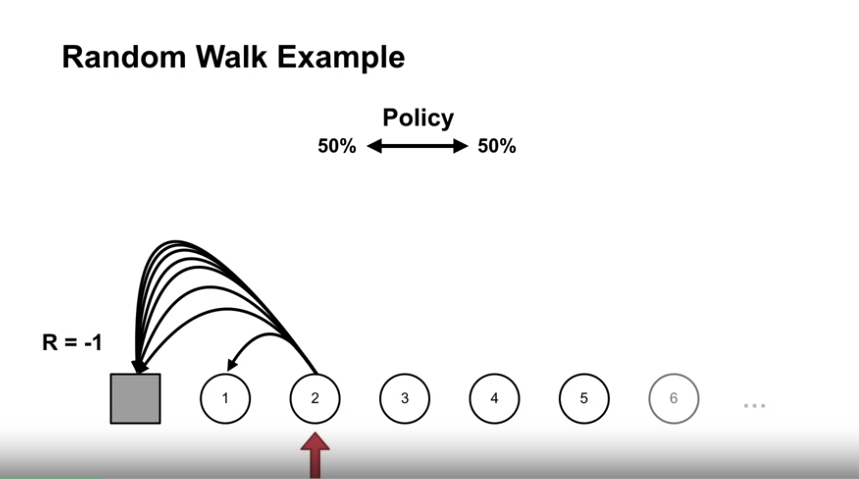
    • 문제의 정의
      • 좌, 우측에 종료상태, 그리고 1 부터 1000 까지의 상태가 있다.
      • 좌측 종료상태에서 보상 -1, 우측 종료상태에서 보상 +1, 그 외의 상태는 보상 0
      • 동작은 좌측 혹은 우측으로 100칸까지 이동 가능하며 좌,우 1~100 칸 이동 확률은 uniform random policy 를 따른다.
      • 첫 시작 지점은 상태 500에서 시작한다.
      • discount gamma 값은 1이다. (할인 없음)

  • State Aggregation

    state_aggregation

    • 몇몇 상태를 같은 상태로 취급하는 기법
    • 위의 예시에서 상태가 8개 있는데, 4개의 상태를 같은 상태로 묶어 2개의 상태로 취급하는 기법임.
      • 즉, 위의 묶음 중 아무 상태가 업데이트 되어도 나머지 3개의 상태가 같이 업데이트된다.
    • State Aggregation 은 linear function approximation 의 일종이다.
    • 상태가 많은 경우 학습의 속도가 느려질 수 있는데, 위 기법을 통해 빠르게 학습할 수 있음.

  • How to Compute the Gradient for Monte Carlo with State Aggregation

    compute_gradient_monte_carlo_with_state_aggregation

  • Constructing a State Aggregation for the Random Walk

    monte_carlo_updates_for_a_single_episode

    • 어떻게 집합으로 묶을 것인가?
      • State Aggregation 은 상태를 동일 그룹 군으로 묶어 같은 가치 추정을 하도록 만든다.
      • 즉, 우리는 상태를 묶을 때 그들의 값이 유사할 것이라고 생각되는 상태들을 그룹군으로 묶어야 한다.
      • 그룹이 작다면 보다 더 정확한 결과를 얻을 것이나, 학습 시간이 더 오래 걸린다.
      • Random Walk 문제에서는 1부터 1000까지의 상태를 100개 단위의 그룹 군으로 묶어본다.

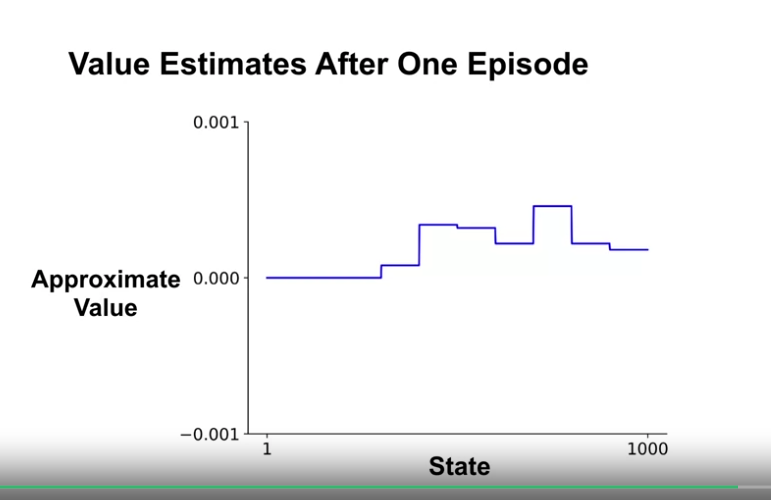
    random_walk_one_episode_result

    • 첫 에피소드에 대한 해석
      • 첫 번째 에피소드는 종료 결과 보상 1을 얻었고, 할인이 없기 때문에 모든 상태에 대한 리턴값은 1이 된다.
      • 속하는 그룹의 가중치 값이 모두 업데이트 된다.
      • 여러 상태를 오간 뒤 첫번째 에피소드에 대한 가치 추정의 결과는 위 그림과 같다.

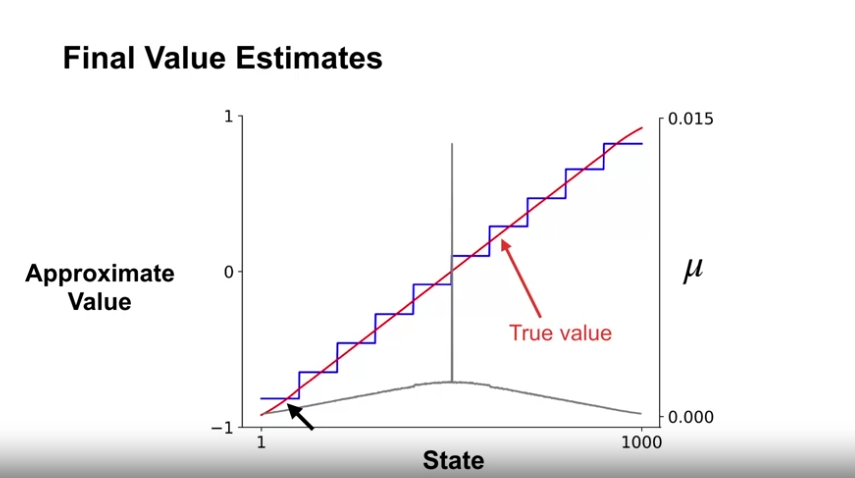
    random_walk_final_value_estimates

    • 최종 에피소드 이후 가치 추정 결과
      • 각 상태그룹에 따라 동일한 근사 값을 가지는 것을 볼 수 있음
      • 참 값이 근사 값의 중앙을 관통하는 것은, 상태의 확률분포 (극단지점의 상태보다 그렇지 않은 상태의 분포가 더 크다) 의 영향이다.

The Objective for TD

Semi-Gradient TD for Policy Evaluation

  • 학습목표
    • 함수 근사를 위한 TD update 의 이해
    • 가치 추정을 위한 Semi-gradient TD(0) 알고리즘의 개요

  • Gradient Monte Carlo 와의 비교

    td_update_for_function_approximation

    • Gradient Monte Carlo 에서는 리턴값 $G_t$ 를 사용하며 이는 편향되지 않은 값이기에 가중치가 지역 최적값에 수렴한다.
      • 꼭 리턴값이 아니더라도 다른 타겟을 사용할 수 있으며, 이 값이 편향되지 않다면 수렴을 보장한다.
    • TD 방식에서는 현재 가치 추정값을 타겟으로 하기에 값이 편향된다.
      • 추정값이기에 참 가치함수와는 값이 다름.
      • 그렇기에 해당 알고리즘은 에러 값이 지역 최소값에 수렴한다고 보장할 수 없다.
  • TD target 의 이점
    • 샘플의 리턴 값보다 분산이 작아 더 빠르게 수렴한다.
  • TD target 의 이점 (Chat GPT)
    • 계산 효율성: 함수 근사를 사용한 TD 업데이트는 매우 큰 상태 공간에서도 적용할 수 있다. 대규모의 상태 공간을 전체적으로 계산하는 것보다 훨씬 효율적임.
    • 활용 가능한 데이터: 실제 상황에서는 종종 완벽한 정보가 제공되지 않는다. 편향된 추정값이라도 현재 사용 가능한 정보를 기반으로 한 업데이트는 여전히 유용할 수 있다.
    • 탐색적인 측면: 편향된 추정값을 사용하는 것은 다양한 상황을 탐색하고 경험하는 데 도움을 줄 수 있다. 이는 종종 실제 환경에서 더 나은 행동을 선택하는 데 도움이 될 수 있다.
    • 일반화 가능성: 함수 근사를 사용한 TD 업데이트는 일반화 가능성을 가질 수 있다. 이는 일부 편향된 추정값이라도 일반적인 상황에서 적용 가능한 모델을 생성할 수 있다는 것을 의미함.

  • TD is a semi-gradient method

    td_is_a_semi_gradient_method

    • TD 의 경우 업데이트의 목표 타겟값이 TD target ($R_{t+1} + \gamma \hat{v} (S_{t+1}, \textbf{w})$) 이다.
    • 목표 타겟값에 가중치 $\textbf{w}$ 가 포함되어 있어, 미분식이 기존의 TD Update 식과 다르게 된다.
      • The TD Update : $-(U_t - \hat{v}(S_t, \textbf{w})) \nabla \hat{v}(S_t, \textbf{w})$
      • 여기에서 TD Update 란 시간차 학습에 의한 실제값과 기대값의 차이를 줄이기 위한 방법을 의미한다.
      • 함수 근사에서 사용될 경우 위와같은 형태가 됨.
    • 즉, 실제 값과 기대값의 차이가 아닌 기대값과 기대값 사이 TD 오차에 비례하는 위의 식은 gradient descent 방법과는 다르다.
    • 위의 차이에도 불구하고, TD 는 많은 케이스에서 수렴한다.

    semi_gradient_td_0_psuedocode

    • Semi-Gradient TD(0) 의 psuedocode
      • TD(0) 는 에피소드가 끝날 때 까지 기다리지 않고, 매 스텝마다 업데이트를 진행한다.

Comparing TD and Monte Carlo with State Aggregation

  • 학습목표
    • TD 가 편항된 가치 추정으로 수렴하는 점을 이해
    • TD 가 Gradient Monte Carlo 보다 훨씬 빠르게 수렴하는 점을 이해

  • Gradient Monte Carlo 의 경우

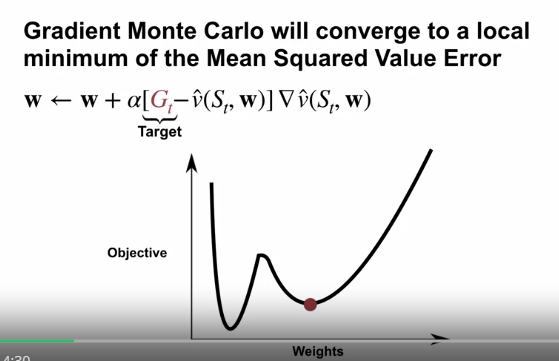
    gradient_monte_carlo_converge_local_minimum

    • 더 많은 샘플들로 최적화 할 수록 Mean Squared Value Error 의 지역최소값에 수렴한다.
    • 이는 value error의 경사로 편향되지 않은 추정값을 사용하기 때문이다.
    • 이론대로라면, 우리는 이 알고리즘을 긴 시간동안, step-size 파라미터를 decay 하며 진행해야 수렴값을 얻을 수 있다.
      • 예제에서 상수 step-size 를 사용하여, 지역 최소값에서 계속 진동하는 것을 볼 수 있다.

  • Semi-Gradient TD 의 경우

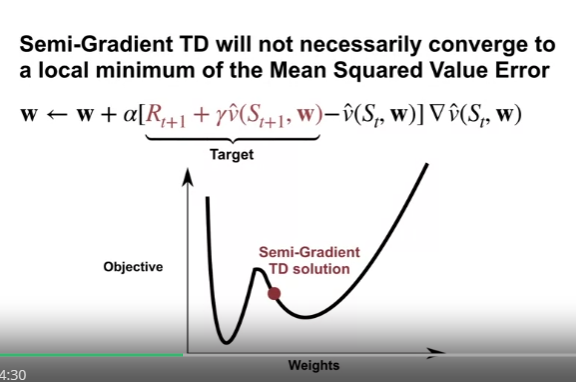
    semi_gradient_td_not_converge_to_a_local_minimum

    • Target 값이 예측값 (정확하지 않은 값) 이므로, 업데이트 값에 편향이 생길 수 있다.
    • 우리의 가치 근사가 경계값 내에서도 완벽할 수 없으므로, Target 은 편향된 상태로 남게 된다.
    • 따라서 Semi-Gradient TD 의 Mean Squared Value Error 가 지역 최소값으로 수렴한다는 것을 보장할 수 없다.
    • 물론 이 편향은 추정이 개선될 수록 줄게 된다.

  • State Aggregation 을 이용한 1000 State Random Walk 문제에서 MC 방식과 TD 방식의 결과 비교

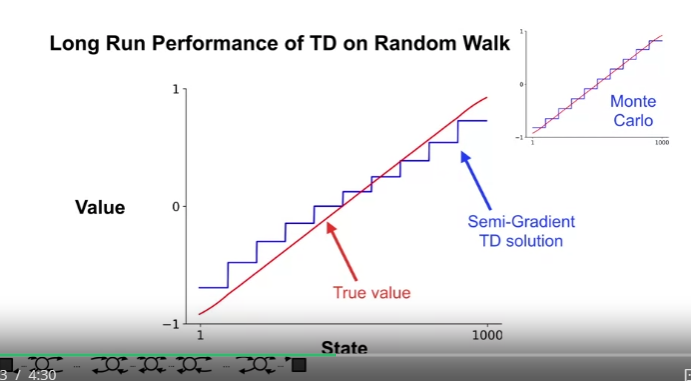
    1000_state_random_walk_semi_gradient_td

    • 1000 State Random Walk 를 값이 수렴할 때까지 진행 (1000 Episodes)
    • Value Estimate 값의 변화가 멈추었을 때의 결과를 도식화함.
    • Monte Carlo 와 비교하여 값이 정확하지 않다. (편향값 때문)

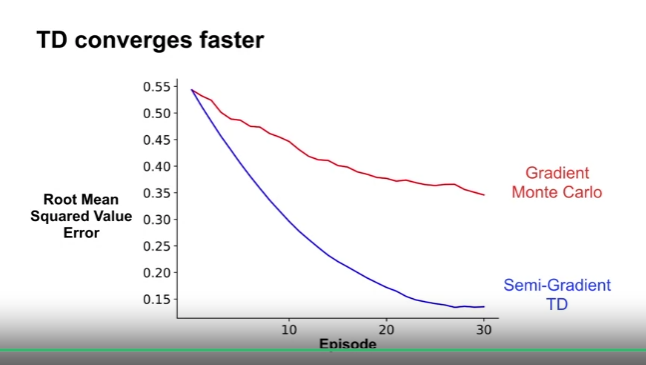
    1000_state_random_walk_30_episodes_td_mc

    • 위 문제를 30 Episodes 만 진행
    • TD 와 MC 의 $\alpha$ 값에 큰 차이가 있으므로, 0과 1 사이의 100개 구간으로 시험하여 가장 좋은 결과의 $\alpha$ 를 선택
      • TD : 0.22
      • MC : 0.01

Doina Precup : Building Knowledge for AI Agents with Reinforcement Learning

  • 강화학습 에이전트가 습득해야 하는 지식의 종류
    • 절차적 지식 (일을 수행하는 방법) - 정책은 이에 해당하는 기본적인 예
    • 우리가 알고 싶어할 수도 있는 다른 지식 - 특정 물체와 상호작용하는 방법, 다른 장소로 이동하는 방법
    • 기술, 옵션, 혹은 목표 지향적인 행동
    • 에이전트의 행동에 따라 어떤 일이 일어날 수 있는지를 의미하는 예측 지식, 경험적 지식
      • 이것은 가치 함수일 뿐만 아니라 모델 예시와 같은 다른 것이기도 하다.
  • 이러한 종류의 지식에 대해 우리가 갖고 싶은 특정 특성
    • 배울만한 지식을 알게 되어, 데이터로부터 그것을 얻고, 표현할 수 있기를 원함
    • 에이전트가 다양한 것, 다양한 상황에 대해 알수 있기를 원하며 이미 가지고 있는 지식 조각을 더 큰 조각으로 구성할 수 있기를 바람
  • 지식 표현의 요소
    • 타임 스케일에 따른 에이전트의 행동 측면에서의 일반화
    • 세상에 대해 인식, 추론하는 에이전트의 능력에서의 일반화
  • 상태 추상화와 함수 근사 (위의 필요성에서 등장)
    • 다른 타임 스케일에서의 절차적 지식의 일반화
      • 에이전트가 생성될 때, 할 수 있는 행동은 제한적이고 이러한 행동들은 항상 한 번의 time step 동안 지속된다.
      • 이는 MDP (Markov Decision Process) 프레임워크와 일치시키기 위한 것이다.
      • 강화학습에서 상태, 행동, 보상 등은 시간 단게에 따라 발생하며 에이전트가 처음 생성될 때 행동의 다양성이나 지속 시간 등이 제한될 수 있다.
  • 에이전트의 행동의 기간을 단일 단계가 아닌 여러 단계로 확장하는 방법
    • 옵션이라는 개념의 사용
      • 초기화 단계 : 옵션이 시작될 수 있는 조건
      • 내부 정책 단계 : 옵션 실행 중 취할 행동
      • 종료 단계 : 언제 종료되는지 결정하는 조건
  • 추상화의 개념으로 본 옵션
    • MDP : 에이전트가 단일 행동에 대한 보상과 상태 전이에 대한 정보를 가지고 있음
    • 옵션 : 일련의 행동들에 대한 일종의 전략이며 각 행동마다 보상과 상태 전이 확률을 내재하고 있는 개념 (행동의 집합, 패턴)
      • 시간의 추상화 : 옵션이 언제 시작되고 언제 종료되는지는 가변적이다. 또한 이를 통해 고정된 time step 에서 벗어나게 된다. (Semi-MDP)
      • 상태의 추상화 : 구체적인 좌표값이 아닌 공항에 대한 추론을 한다.
      • 행동의 추상화 : 각 근육의 조절이 아닌 공항으로 가는 행동에 대해 생각한다.
      • 이는 MDP에서의 행동보다는 더 큰 시간적, 행동적, 그리고 상태적인 추상화 수준을 제공한다.
      • 위의 추상 항목들은 모두 별개이며 함께 잘 작동하도록 조율하는 방법은 연구가 필요한 문제이다.
  • 옵션을 학습하는 강화학습 방법
    • 어떤 옵션을 사용할지 또한 선택이며, 이 또한 학습의 대상이다.
    • 옵션을 학습하는 강화학습 방법 중 하나, “Option-Critic Architecture”
      • 옵션 선택기 (Option Selector): 에이전트가 주어진 상태에서 어떤 옵션을 선택할지 결정하는 부분. 이 선택기는 가능한 옵션들의 가치를 추정하여 가치가 높은 옵션을 선택하도록 학습됨
      • 옵션 평가자 (Option Evaluator): 선택된 옵션이 얼마나 좋은지, 즉 해당 옵션의 예상 보상이 어떤지를 평가하는 부분. 이 평가자는 선택된 옵션의 가치를 추정하고, 이를 통해 선택된 옵션이 잘 수행될 것인지를 예측함.
      • 이 아키텍처를 통해 옵션 선택과 평가를 결합하여 옵션을 효과적으로 학습하고 발전시킬 수 있다. 이러한 접근 방식은 여러 상황에서의 옵션 선택과 실행에 대한 전략을 효과적으로 학습하고 조정할 수 있도록 돕는다.

Linear TD

The Linear TD Update

  • 학습목표
    • 선형 함수 근사 를 사용하여 TD-update 도출
    • tabular TD(0) 가 linear semi-gradient TD(0) 의 특별한 케이스인 것을 이해하기
    • 왜 linear TD 를 특수 케이스로 취급하는지 이해하기

  • TD Update with Linear Function Approximation

    td_update_with_linear_function_approximation

    • 가중치를 해당 가중치에 해당하는 TD error 와 근사가치함수의 경사값의 곱의 값에 따라 조절한다.
    • 이 때, 근사가치함수의 경사값은 선형 가치근사함수에 의해 feature vector 의 값이 된다.
      • feature 값이 크면 큰 영향을 주게 되고, feature 값이 0이면, 아무런 영향을 주지 않는다.
    • 즉 선형가치근사함수의 경우 feature 값이 잘 선택되면 효율적으로 작동한다.

  • Tabular TD is a special case of linear TD

    tabular_td_is_a_special_case_of_linear_td

    • 위의 식과 같이 모든 상태에 대해 각각의 대응하는 가중치값이 존재한다면, 이는 tabular td 와 동일한 형태가 된다.
  • 선형함수근사의 유용성
    • 선형 방식은 이해하기 쉽고 수학적으로 분석이 가능하다.
    • 좋은 feature 가 있으면 선형 방식은 학습도 빠르고 좋은 예측 정확도를 보여줄 수 있다.

The True Objective for TD

  • 학습목표
    • linear TD 학습의 고정점 (fixed point) 에 대해 이해
    • TD 고정점에서 평균 제곱 오차의 이론적 보증에 대한 설명

  • The Expected TD Update

    linear_function_approximation_expected_td_update

    • 위 Expected TD Update 식은 아래의 연산규칙에 의해 변형이 가능하다.
      • 위 식에 사칙연산 중 분배법칙이 성립한다.
      • 스칼라 값 (벡터간 내적곱) 은 전치해도 식이 변형되지 않는다.
    • 위의 규칙에 의해 변형된 식에 대해서
      • Matrix A : feature 에 대한 기대값
      • vector b : feature 와 보상에 대한 항

  • The TD Fixed Point

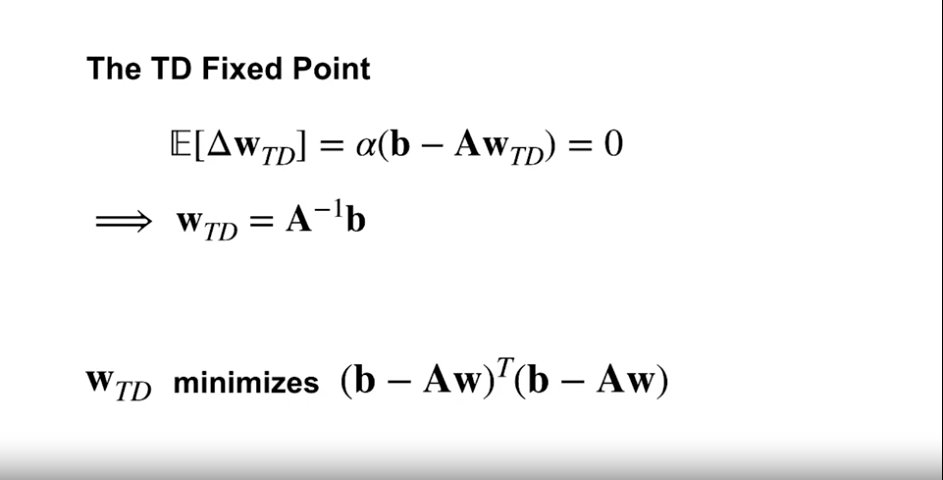
    linear_function_approximation_td_fixed_point

    • TD 업데이트가 선형인 경우
      • 테이블 설정에서 벨만 방정식을 해결하는 것이 아닌 (샘플데이터 사용)
      • 해(solution)를 수식으로 구하는 방식인 선형 TD에 대해 설명하고 있음.
      • 선형 TD는 TD 업데이트를 선형 함수로 근사하며, 이를 사용하여 벨만 방정식의 해를 직접 구한다.
    • 여기서 해(solution)는 TD 고정점(TD fixed point)을 의미한다.
      • 이 해는 평균 제곱 오차(Mean Squared Value Error)의 최소값으로 수렴하지는 않지만
      • TD의 목적 함수에 기반한 원칙적인 최소값으로 수렴한다는 것을 설명하고 있다.
      • 따라서 TD의 학습 목표는 평균 제곱 오차의 최소값이 아닌, 벨만 방정식과 관련된 목적 함수의 최소값을 찾는 것이 된다.

  • TD Fixed Point 와 Minimum of the Value Error 의 관계

    linear_function_approximation_td_fixed_point_and_minimum_ve

    • 그럼에도 불구하고, 우리는 여전히 TD에 의해 찾아진 해와 오류를 최소 값으로 만드는 해 사이의 관계를 알고 싶음.
      • 위 방정식과 같이 $\gamma$ 가 0에 매우 가깝다면, TD Fixed Point 는 Minimum of the Value Error 의 해와 매우 가까워짐
    • Feature 의 품질과도 연관이 있는데, Feature 가 제한적이라면 TD Fixed Point 나 Minimum of the Value Error 또한 커지게 됨.
      • 만약 가치함수를 완벽하게 나타낼 수 있다면, $\gamma$ 와 무관하게 TD Fixed Point 는 Minimum of the Value Error 와 동일하게 됨.
      • 양쪽 모두가 0 가 되기 때문
    • TD Fixed Point 와 Minimum of the Value Error 의 해와 차이가 발생하는 이유
      • 함수 근사값의 부트스트래핑 목표를 사용하기 때문
      • 다음 상태에 대한 추정이 함수 근사로 인해 지속적으로 부정확하다면, 부정확한 대상을 향해 업데이트 됨.
      • 만약 함수 근사가 좋다면 다음 상태에 추정값은 매우 정확해짐.

댓글남기기

참고